6.4.2 Angles and Tangents of Circles (Sample Questions) - Mathematics

Example 1:

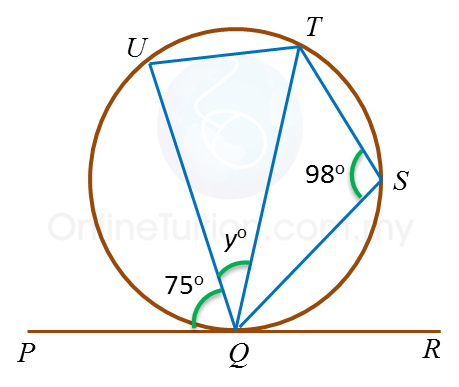
In the diagram, PQR is a tangent to the circle QSTU at Q.

Find the value of y.

Solution:

Angle QUT

= 180^o– 98^o ← (opposite angle in cyclic quadrilateral QSTU )

= 82^o

Angle QTU = 75^o ← (angle in alternate segment)

Therefore y= 180^o – (82^o + 75^o) ← (Sum of interior angles in ∆ QTU)

= 23^o

Example 2:

In the diagram, PQR is a tangent to the circle QSTU at Q.

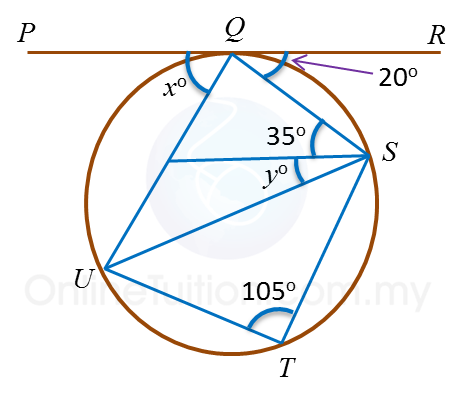
Find the values of

(a) x (b) y

Solution:

(a)

∠UTS + ∠UQS = 180^o ←(opposite angle in cyclic quadrilateral QSTU)

105^o + ∠ UQS = 180^o

∠ UQS = 75^o

x+ 75^o + 20^o = 180^o←(the sum of angles on a straight line PQR = 180^o)

x+ 95^o = 180^o

x = 85^o

(b)

∠ PQU = ∠ QSU ← (angle in alternate segment)

85^o = 35^o + y

y = 50^o

Example 3:

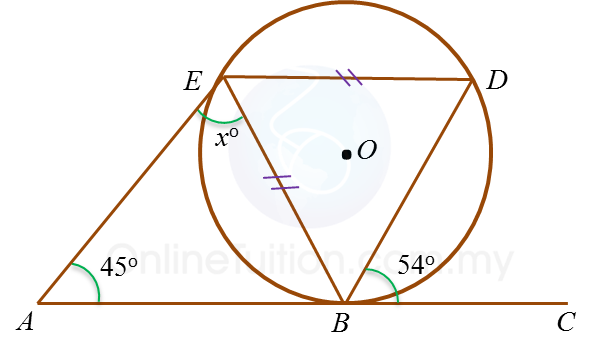
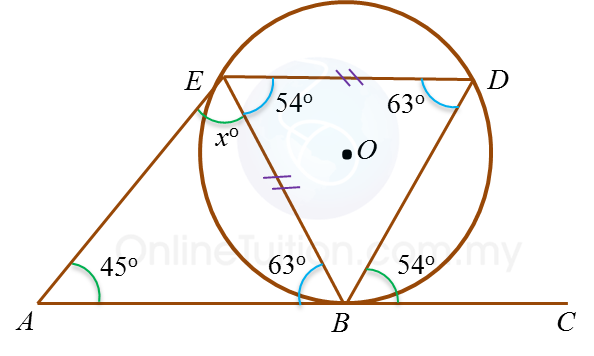
In the diagram, ABC is a tangent to the circle BDE with centre O, at B.

Find the value of x.

Solution:

\begin{array}{l} ∠ B E D = ∠ C B D = 54^{\circ} \\ ∠ B D E = \frac{180^{\circ} - 54^{\circ}}{2} = 63^{\circ} \leftarrow \begin{array}{l} Isosceles triangle \\ ∠ E B D = ∠ E D B \end{array} \\ ∠ A B E = ∠ B D E = 63^{\circ} \\ In △ A B E, \\ x^{\circ} + 45^{\circ} + 63^{\circ} = 180^{\circ} \\ x^{\circ} + 108^{\circ} = 180^{\circ} \\ x = 72 \end{array}