6.4.1 Angle between Tangent and Chord
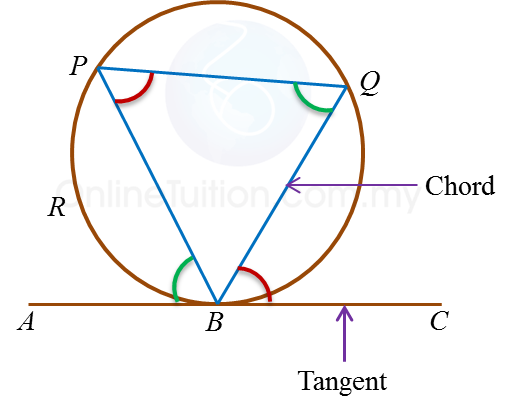
1. In the diagram above, ABC is a tangent to the circle at point B.
2. Chord PB divides the circle into two segments, that is, the minor segment PRB and the major segment PQB.
3. With respect to ∠PBA, ∠PQB is known as the angle subtended by chord BP in the alternate segment.
4. With respect to ∠QBC, ∠BPQ is known as the angle subtended by chord BQ in the alternate segment.
5. The angle formed by the tangent and the chord which passes through the point of contact of the tangent is the same as the angle in the alternate segment which is subtended by the chord.
6. The relationships between the angles are:
Angle ∠ABP = Angle ∠BQP
Angle ∠CBQ = Angle ∠BPQ
Example:
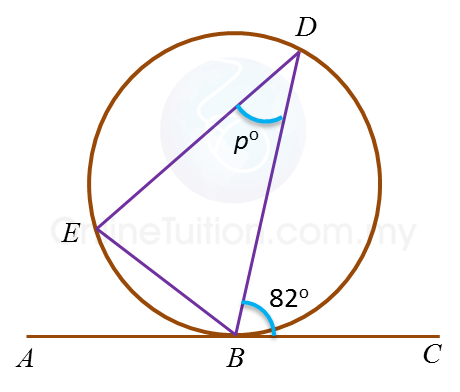

In the diagram, ABC is a tangent to the circle BDE at B.
The length of arc BD is equal to the length of arc DE.
Find the value of p.
Solution:
Angle BED = 82o ← (angle in alternate segment)
Angle DBE = 82o ← (Arc BD = Arc DE, BDE is an isosceles triangle)
Therefore p= 180o – 82o – 82o = 16o