10.4.2 Gradient of a Straight Line, PT3 Focus Practice


Question 6:
Diagram below shows a straight line RS with equation 3y = –px – 12, where p is a constant.
 

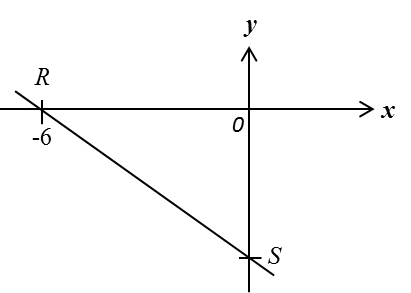
It is given that OR: OS = 3 : 2.
Find the value of p.


Solution:
Method 1:
Substitute x= –6 and y = 0 into 3y = –px – 12:
3(0) = –p (–6) – 12
0 = 6p – 12
–6p = –12
p = 2

Method 2:
OR: OS = 3 : 2
O R O S = 3 2 6 O S = 3 2 O S = 6 × 2 3 = 4 units  

Coordinates of S = (0, –4)
Gradient of the straight line RS = − − 4 − 6 = − 2 3  

Given 3y = –px – 12
Rearrange the equation in the form y = mx + c
y = − p 3 x − 4 Gradient of the straight line R S = − P 3 ∴ − P 3 = − 2 3 P = 2




Question 7:

 
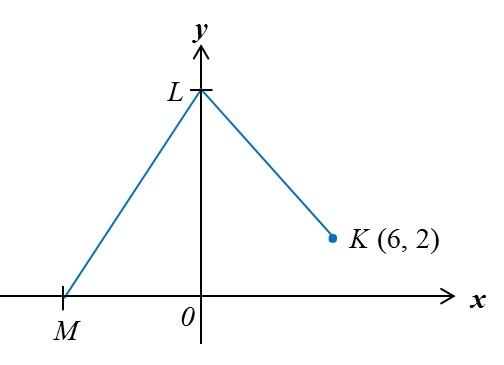
The above diagram shows two straight lines, KL and LM, on a Cartesian plane. The distance KL is 10 units and the gradient of LM is 2. Find the x-intercept of LM.


Solution:


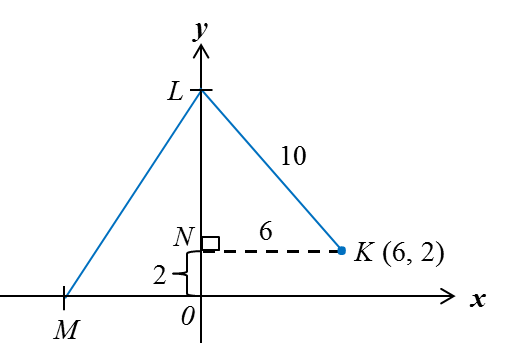
Let point N be = (0, 2).
Using Pythagoras’ Theorem,
 LN = √102 – 62 = 8
Point L = (0, 2 + 8) = (0, 10)
y-intercept of LM = 10
 
Using the gradient formula, m = − y-intercept x-intercept 2 = − ( 10 x-intercept ) x-intercept of L M = − 10 2 = − 5  

Leave a Comment