11.1 Isometric Transformations
11.1.1 Transformation
11.1.2 Translation
1. A translation is a transformation which moves all the points on a plane through the same distance in the same direction.
2. Under a translation, the shape, size and orientation of object and its image are the same.
3. A translation in a Cartesian plane can be represented in the form
whereby, a represents the movement to the right or left which is parallel to the x-axis and b represents the movement upwards or downwards which is parallel to the y-axis.
Example 1:
Write the coordinates of the image of A (–2, 4) under a translation
and B (1, –2) under a translation
.
Solution:
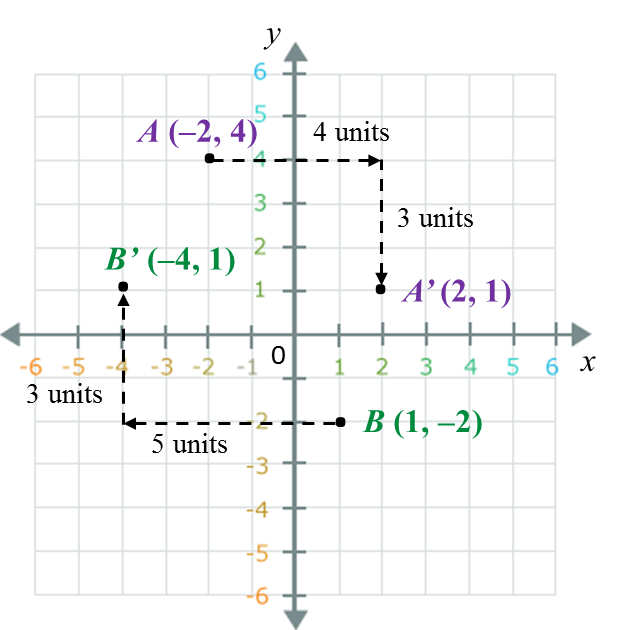
A’ = [–2 + 4, 4 + (–3)] = (2, 1)
B’ = [1 + (–5), –2 + 3] = (–4, 1)
Example 2:
Point K moved to point K’ (3, 8) under a translation
What are the coordinates of point K?
Solution:
The coordinates of K = [3 – (– 4), 8 – 3]
= (7, 5)
Therefore the coordinates of K are (7, 5).
can you double check the example 2 ?? I think there was some mistake in the equation