Question 6:
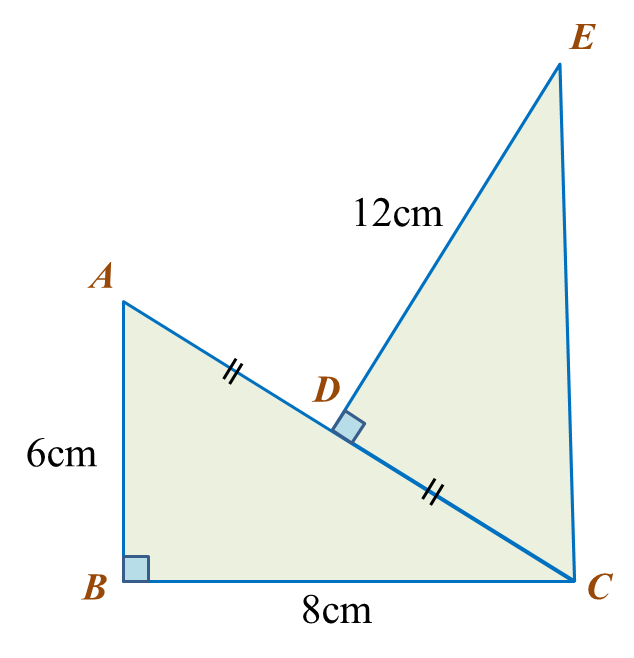

In the diagram shows two right-angled triangles. Calculate the perimeter of the whole diagram.
Solution:
In ∆ ABC,
AC2 = 62 + 82
= 36 + 64
= 100
AC = √100
= 10 cm
AD = 5 cm
In ∆ EDC,
EC2 = 122 + 52
= 144 + 25
= 169
EC = √169
= 13 cm
Perimeter of the whole diagram
= AB + BC + CE + DE + AD
= 6 + 8 + 13 + 12 + 5
= 44 cm
Question 7:
In the diagram, ABCD is a trapezium and AED is a right-angled triangle.
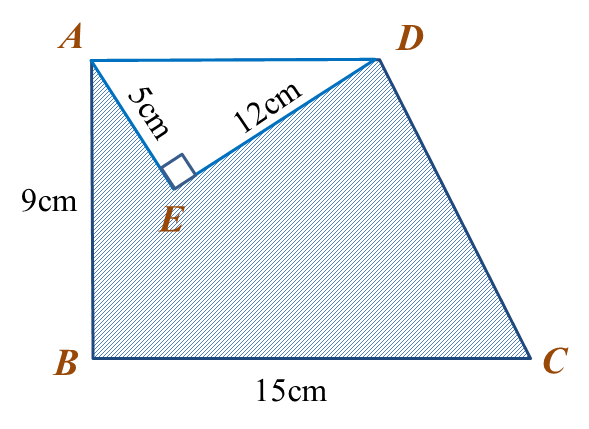
Calculate the area, in cm2, of the shaded region.
Solution:
AD2 = 52 + 122
= 25 + 144
= 169
AD = √169
= 13 cm
Area of trapezium ABDC
= ½ (13 + 15) × 9
= 126 cm2
Area of triangle AED
= ½ × 5 × 12
= 30 cm2
Area of the shaded region
= 126 – 30
= 96 cm2