Question 3:
In diagram below, ABCH is a square and DEFG is a rectangle. HCDE is a straight line and HC = CD.
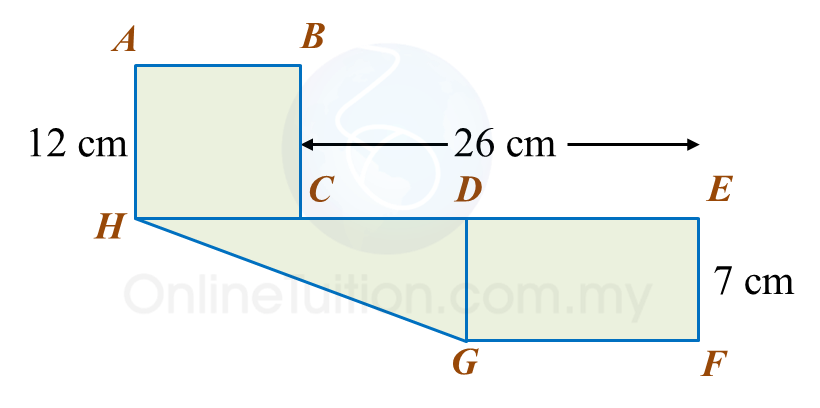
Find the perimeter, in cm, of the whole diagram.
Solution:
G H 2 = D H 2 + D G 2 = 24 2 + 7 2 = 576 + 49 = 625 G H = 25 cm Perimeter of the whole diagram = 12 + 12 + 12 + 26 + 7 + 14 + 25 = 108 cm
In diagram below, ABCH is a square and DEFG is a rectangle. HCDE is a straight line and HC = CD.

Find the perimeter, in cm, of the whole diagram.
Solution:
Question 4:
In the diagram, ABC and EFD are right-angled triangles.

Calculate the perimeter, in cm, of the shaded region.
Solution:
D E 2 = 3 2 + 4 2 = 9 + 16 = 25 D E = 25 = 5 cm A C 2 = 7 2 + 24 2 = 49 + 576 = 625 A C = 625 = 25 cm Perimeter of the shaded region = 24 + 7 + ( 25 − 5 ) + 3 + 4 = 58 cm
In the diagram, ABC and EFD are right-angled triangles.

Calculate the perimeter, in cm, of the shaded region.
Solution:
Question 5:
In the diagram, ABD and BCE are right-angled triangles. ABC and DBE are straight lines. The length of AB is twice the length of BC.
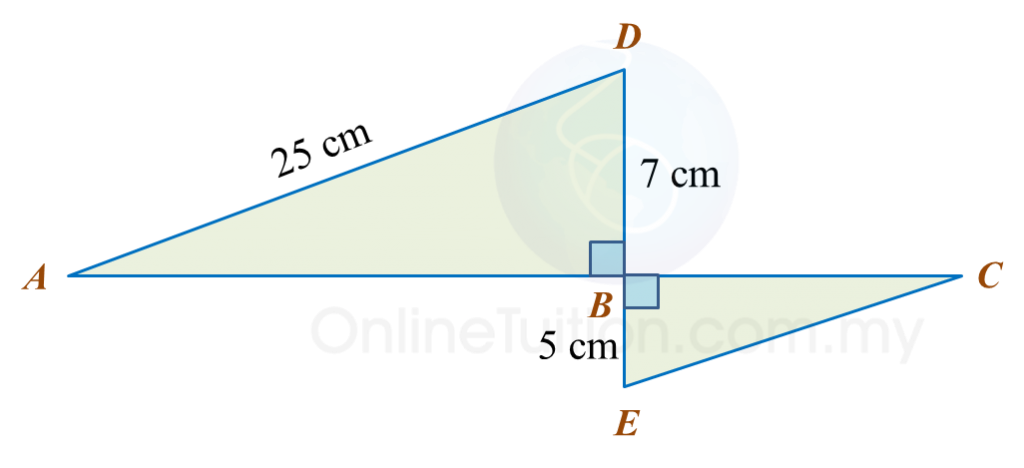
Calculate the length, in cm, of CE.
Solution:
A B 2 = 25 2 − 7 2 = 625 − 49 = 576 A B = 576 = 24 cm B C = 24 cm ÷ 2 = 12 cm C E 2 = 5 2 + 12 2 = 25 + 144 = 169 C E = 169 = 13 cm
In the diagram, ABD and BCE are right-angled triangles. ABC and DBE are straight lines. The length of AB is twice the length of BC.

Calculate the length, in cm, of CE.
Solution: