13.2.4 The Pythagoras’ Theorem, PT3 Focus Practice - Mathematics

Question 8:

In diagram below ABDE is a square and EDC is a straight line.

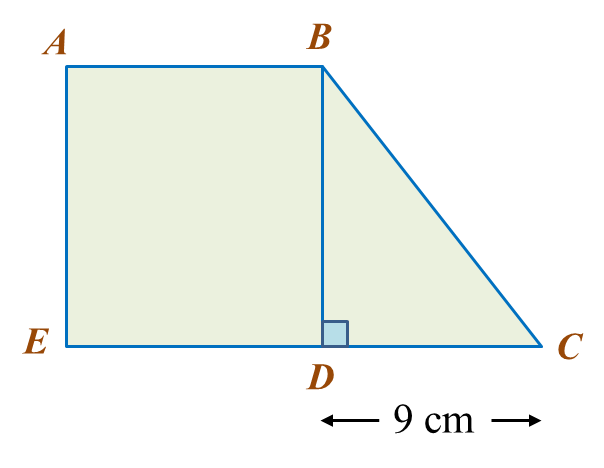
The area of the square ABDE is 144 cm².

Calculate the length, in cm, of BC.

Solution:

BD = √144

= 12 cm

BC²= 12² + 9²

= 144 + 81

= 225

BC = √225

= 15 cm

Question 9:
Diagram below shows two right-angled triangles, ABE and CBD. BED is a straight line.

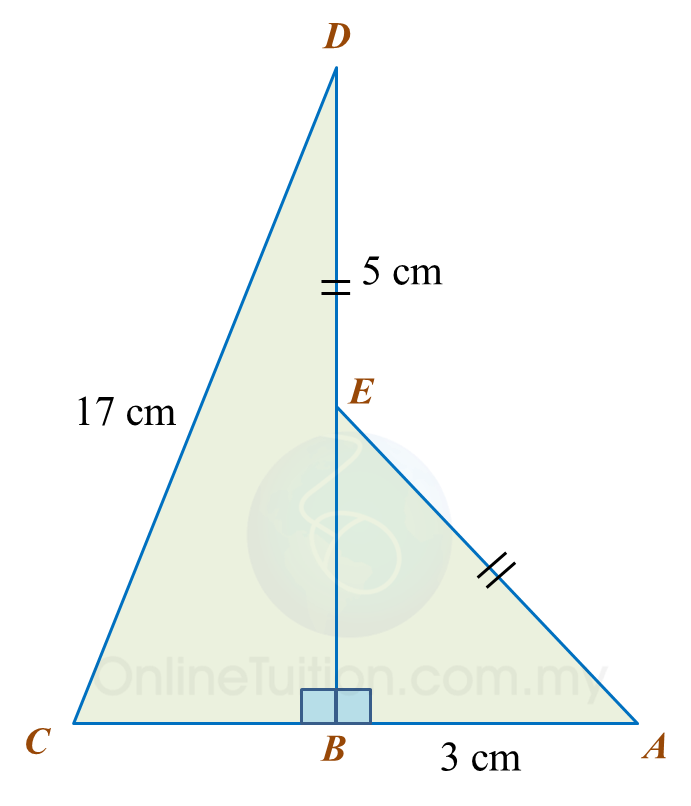Find the length, in cm, of BC. Round off the answer to two decimal places.

Solution:

$\begin{array}{l} 3^{2} + B E^{2} = 5^{2} \\ B E^{2} = 5^{2} - 3^{2} = 16 \\ B E = 4 cm \\ B C^{2} + {(5 + 4)}^{2} = 17^{2} \\ B C^{2} = 17^{2} - 9^{2} = 208 \\ B C = \sqrt{208} \\ B C = 14.42 cm \end{array}$

Question 10:
Diagram below shows two right-angled triangles, ABC and ADE. ACD is a straight line.

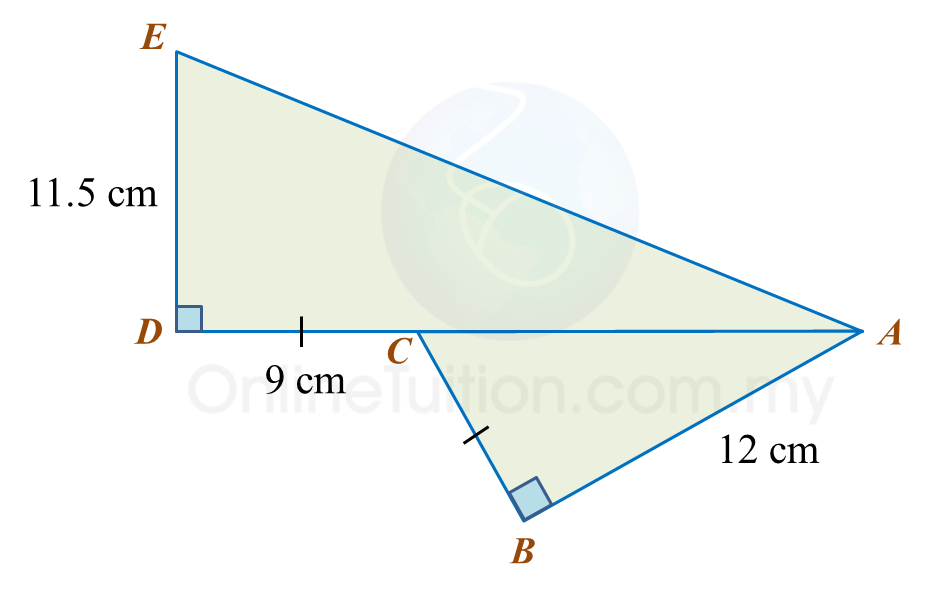Find the length, in cm, of AE. Round off the answer to one decimal places.

Solution:

$\begin{array}{l} A C^{2} = 12^{2} + 9^{2} \\ = 225 \\ A C = \sqrt{225} \\ = 15 cm \\ A E^{2} = {(15 + 9)}^{2} + {11.5}^{2} \\ = 576 + 132.25 \\ = 708.25 \\ A E = \sqrt{708.25} \\ = 26.6 cm \end{array}$

Leave a Comment Cancel reply