Question 2 (a):
(i) Name one angle which is equal to angle d.
(ii) Find the value of angle j.
Solution:
(i)
d = f
(ii)
j + 108 = 180
j = 180 – 108
j = 72
(i) Name one angle which is equal to angle d.
(ii) Find the value of angle j.
Solution:
(i)
d = f
(ii)
j + 108 = 180
j = 180 – 108
j = 72
Question 2 (b):
Statement:
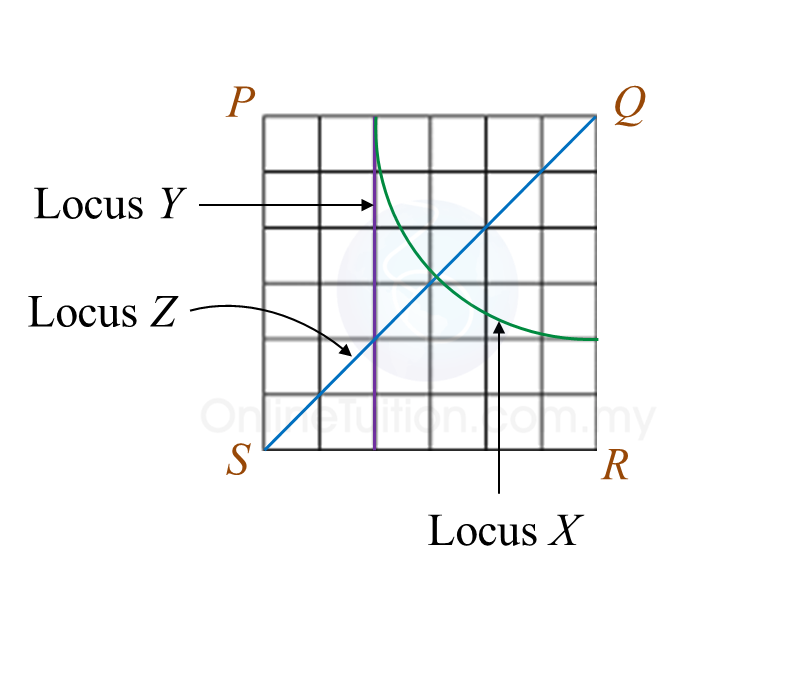
(i) Locus X is a moving point such that its distance is constantly 4 units from point Q.
(ii) Locus Y is a moving point such that its perpendicular distance is always 2 units from line PS.
(iii) Locus Z is a moving point such that it is always equidistant from point P and point R.
In the answer space, draw the locus for each of the given statement on squares grid of 1 unit.
Answer:
Solution:
Statement:
(i) Locus X is a moving point such that its distance is constantly 4 units from point Q.
(ii) Locus Y is a moving point such that its perpendicular distance is always 2 units from line PS.
(iii) Locus Z is a moving point such that it is always equidistant from point P and point R.
In the answer space, draw the locus for each of the given statement on squares grid of 1 unit.
Answer:
Solution:Question 2 (c):
(i) Solve: 5(3 + x) = 20x
(ii) In Diagram 2.2, ABCD is a trapezium and EFG is an equilateral triangle. The perimeter of trapezium ABCD is equal to the perimeter of triangle EFG.
Find the value of w.
Solution:
(i)
5(3 + x) = 20x
15 + 5x = 20x
15x = 15
x = 1
(ii)
Perimeter ABCD = Perimeter EFG
w + 6 + 9 + 2w + 9 = 3 × 20
3w + 24 = 60
3w = 36
w = 12
(i) Solve: 5(3 + x) = 20x
(ii) In Diagram 2.2, ABCD is a trapezium and EFG is an equilateral triangle. The perimeter of trapezium ABCD is equal to the perimeter of triangle EFG.
Find the value of w.Solution:
(i)
5(3 + x) = 20x
15 + 5x = 20x
15x = 15
x = 1
(ii)
Perimeter ABCD = Perimeter EFG
w + 6 + 9 + 2w + 9 = 3 × 20
3w + 24 = 60
3w = 36
w = 12