Question 4:
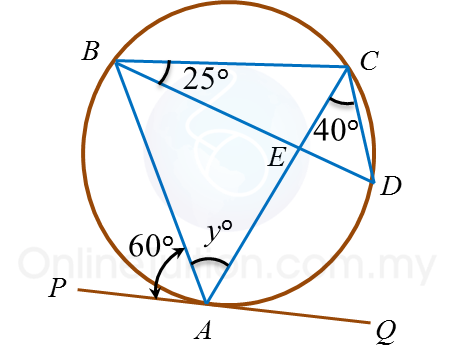

In figure above, PAQ is a tangent to the circle at point A. AEC and BED are straight lines. The value of y is
Solution:
∠ABD = ∠ACD = 40o
∠ACB = ∠PAB = 60o
y= 180o – ∠ACB – ∠CBD – ∠ABD
y= 180o – 60o – 25o– 40o = 55o
Question 5:
Solution:

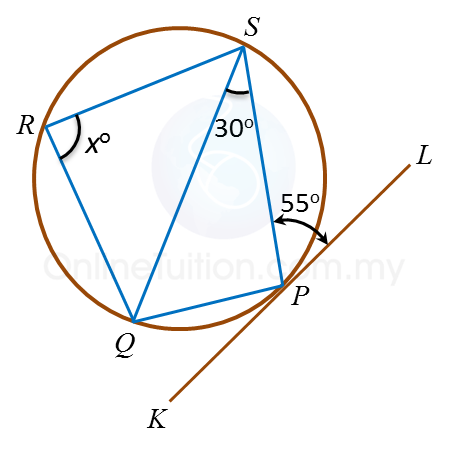
In figure above, KPL is a tangent to the circle PQRS at point P. The value of x is
Solution:
∠PQS = ∠SPL= 55o
∠SPQ = 180o – 30o – 55o= 95o
In cyclic quadrilateral,
∠SPQ + ∠SRQ = 180o
95o+ xo = 180o
x = 85o
Question 6:
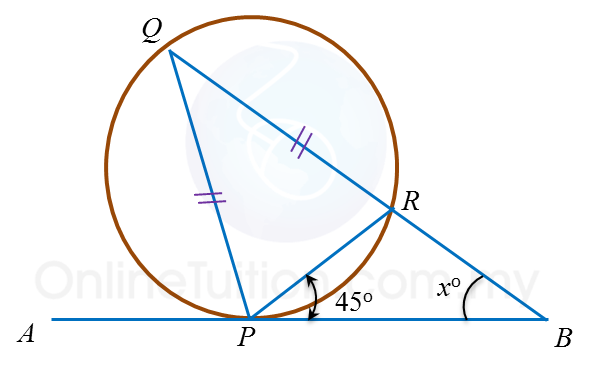

In figure above, APB is a tangent to the circle PQR at point P. QRB is a straight line. The value of x is
Solution:
∠PQR = ∠RPB = 45o
∠QPR = (180o – 45o) ÷ 2 = 67.5o
∠PQR + ∠BPQ + xo = 180o
45o + (67.5o + 45o) + xo = 180o
x = 22.5o