6.7.1 Angles and Tangents of Circles, PT3 Focus Practice - Mathematics

Question 1:

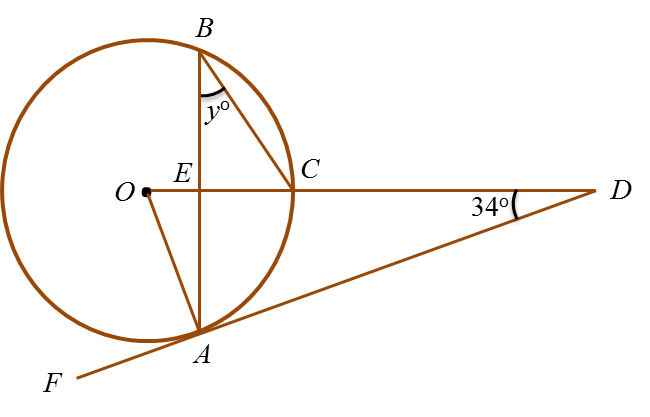
In figure above, FAD is a tangent to the circle with centre O. AEB and OECD are straight lines. The value of y is

Solution:

∠OAD = 90^o

∠AOD= 180^o– 90^o – 34^o= 56^o

y = 56^o÷ 2 = 28^o

Question 2:

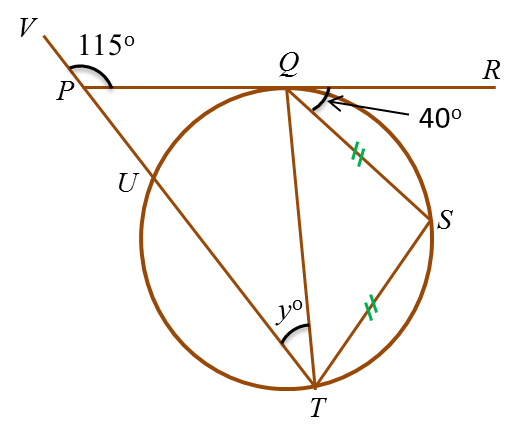
In figure above, PQR is a tangent to the circle QSTU at Q and TUPV is a straight line. The value of y is

Solution:

∠QTS = ∠RQS = 40^o

∠SQT= ∠QTS = 40^o (isosceles triangle)

∠PQT= 180^o– 40^o – 40^o= 100^o

∠TPQ= 180^o– 115^o = 65^o

y = 180^o– 100^o – 65^o= 15^o

Question 3:

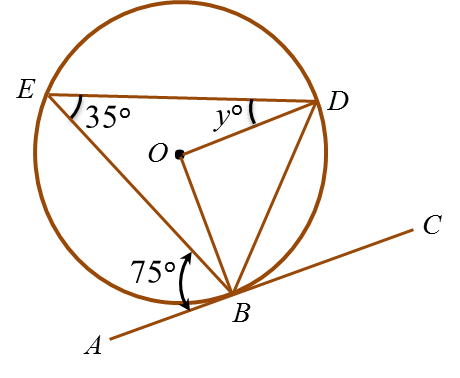
In figure above, ABC is a tangent to the circle BDE with centre O, at B.

Find the value of y.

Solution:

∠BOD= 2 × ∠BED

= 2 × 35^o = 70^o

∠ODB = ∠OBD

= (180^o– 70^o) ÷ 2 = 55^o

∠ EDB = ∠ EBA = 75^o

y^o+ ∠ ODB = 75^o

y^o+ 55^o = 75^o

y= 20^o