Question 4 (a):
(i) Circle the algebraic expression which has three terms.
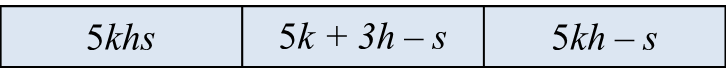
(ii) Fill in the blank with the correct common factor.

(iii) Simplify:
5a – 1 + a
Solution:
(i)
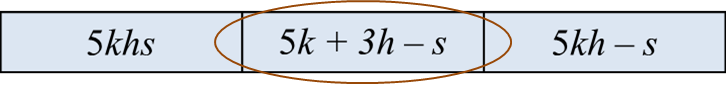
(ii)
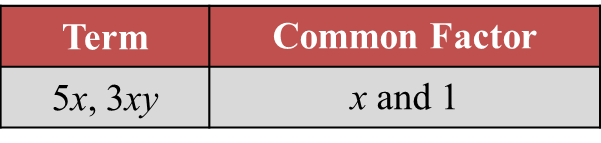
(iii)
5a – 1 + a
= 5a + a – 1
= 6a – 1
(i) Circle the algebraic expression which has three terms.
(ii) Fill in the blank with the correct common factor.

(iii) Simplify:
5a – 1 + a
Solution:
(i)
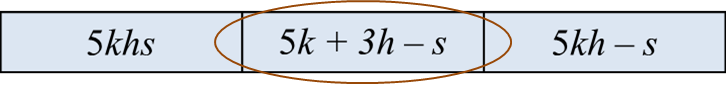
(ii)
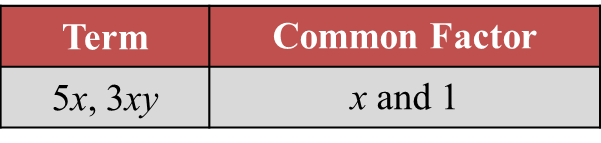
(iii)
5a – 1 + a
= 5a + a – 1
= 6a – 1
Question 4 (b):
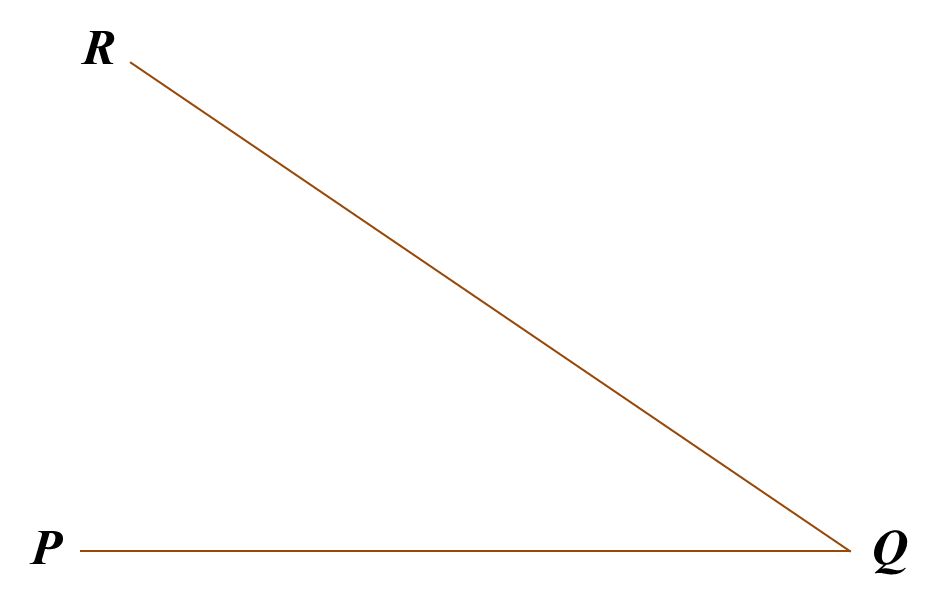
(i) Measure the acute angle of the ∠PQR using a protractor.
Answer:
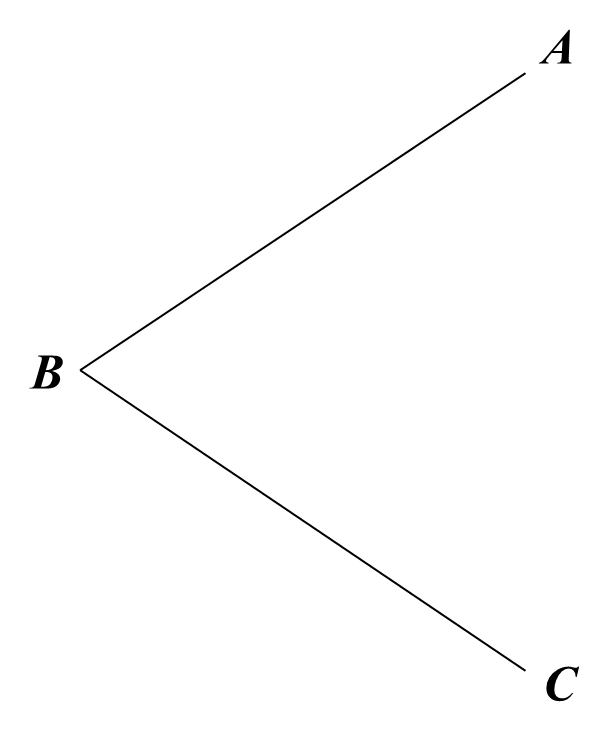
(ii) Construct the angle bisector of ABC.
Answer:
(iii) Construct the angle of 120o at A.
Answer:

Solution:
(i)
∠PQR = 35o
(ii)
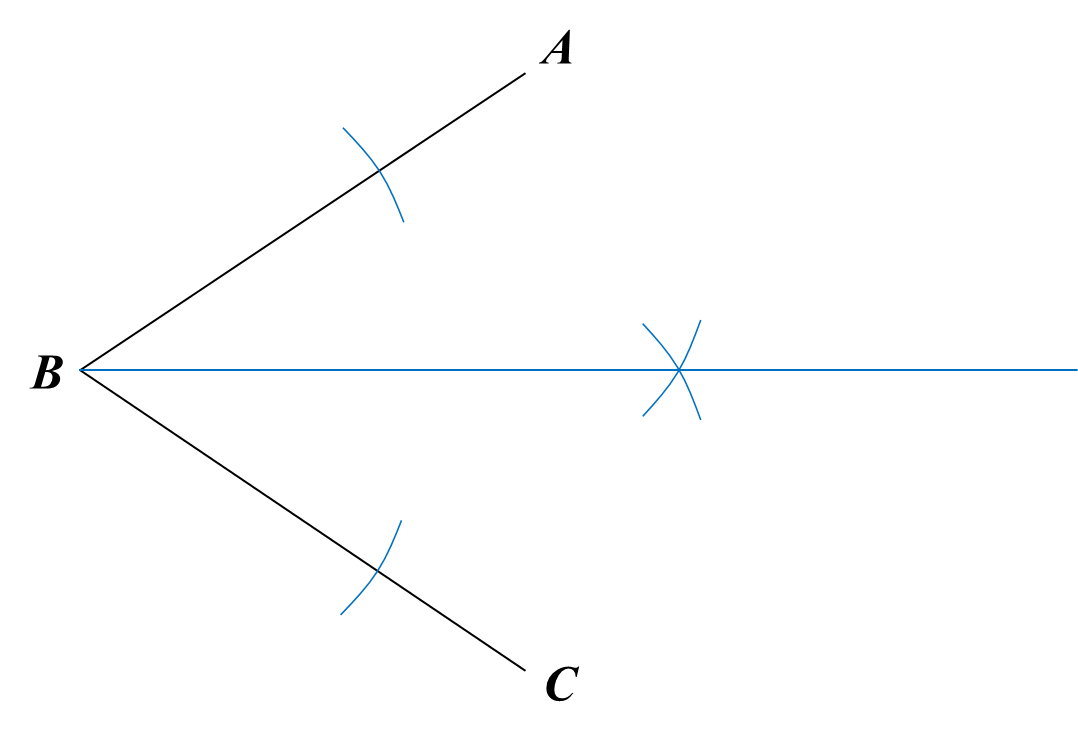
(iii)

(i) Measure the acute angle of the ∠PQR using a protractor.
Answer:

(ii) Construct the angle bisector of ABC.
Answer:

(iii) Construct the angle of 120o at A.
Answer:

Solution:
(i)
∠PQR = 35o
(ii)

(iii)

Question 4 (c):
(i) Diagram 4.1 shows a circle. Arc QR and arc ST are equal in length.
 Calculate the value of y.
Calculate the value of y.
(ii) Diagram 4.2 shows a sector AOB with centre O and the length of arc AB is 11 cm.
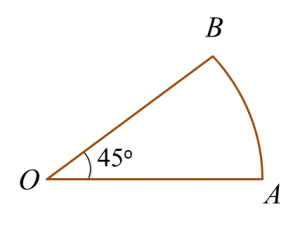 Calculate the radius, in cm, of sector AOB.
Calculate the radius, in cm, of sector AOB.
[ Use π = 22 7 ]
Solution:
(i)
y + 35 o + 25 o = 180 o y = 180 o − 60 o y = 120 o
(ii)
Arc length A B = x 360 × 2 π r 11 = 45 360 × 2 × 22 7 × r 11 = 11 14 r r = 14 11 × 11 r = 14 cm
(i) Diagram 4.1 shows a circle. Arc QR and arc ST are equal in length.
 Calculate the value of y.
Calculate the value of y.(ii) Diagram 4.2 shows a sector AOB with centre O and the length of arc AB is 11 cm.
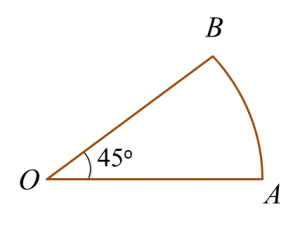 Calculate the radius, in cm, of sector AOB.
Calculate the radius, in cm, of sector AOB.Solution:
(i)
(ii)