Question 6 (a):
(i) Fill in the blanks with the correct answer.

(ii) Diagram 6.1 shows a set of triangles.
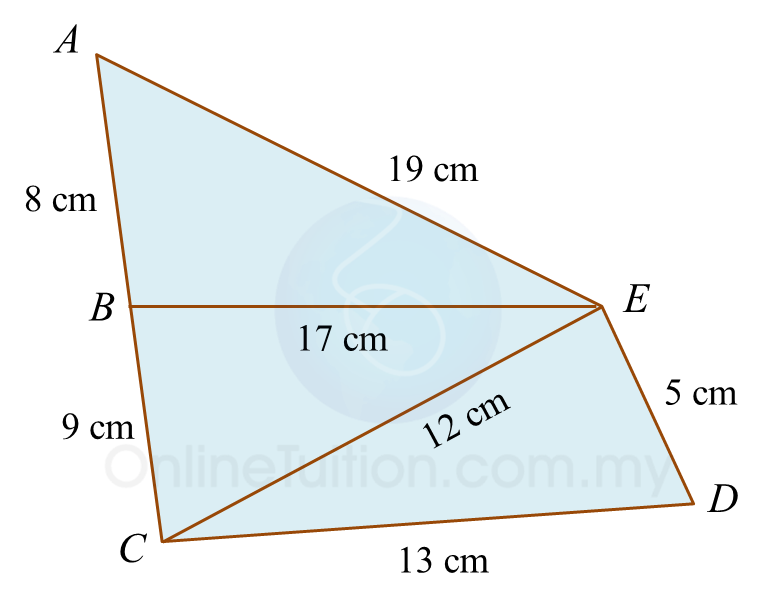
On the answer space, mark (\/) for the right-angled triangles and mark (x) for the not right-angled triangles.
Answer:
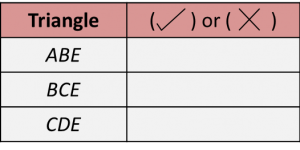
Solution:
(i)
(ii)
In ∆ABE,
AE2 = AB2 + BE2
= 8 2 + 172
= 353
≠ 192
Therefore, ∆ABE is not a right-angled triangle.
In ∆BCE,
BE2 = BC2 + CE2
= 9 2 + 122
= 152
≠ 172
Therefore, ∆BCE is not a right-angled triangle.
In ∆CDE,
CD2 = CE2 + DE2
= 12 2 + 52
= 169
= 132
Therefore, ∆CDE is a right-angled triangle.
(i) Fill in the blanks with the correct answer.

(ii) Diagram 6.1 shows a set of triangles.

On the answer space, mark (\/) for the right-angled triangles and mark (x) for the not right-angled triangles.
Answer:

Solution:
(i)
(ii)
In ∆ABE,
AE2 = AB2 + BE2
= 8 2 + 172
= 353
≠ 192
Therefore, ∆ABE is not a right-angled triangle.
In ∆BCE,
BE2 = BC2 + CE2
= 9 2 + 122
= 152
≠ 172
Therefore, ∆BCE is not a right-angled triangle.
In ∆CDE,
CD2 = CE2 + DE2
= 12 2 + 52
= 169
= 132
Therefore, ∆CDE is a right-angled triangle.

Question 6 (b):
Diagram 6.1 shows a polygon.

(a) If the polygon is redrawn using the scale 1 : 500, calculate the length of side drawn for the side 15 m.
(b) On the square grids in the answer space, redraw the polygon using the scale 1 : 500. The grid has equal squares with sides of 1 cm.
Solution:
(a)
(b)
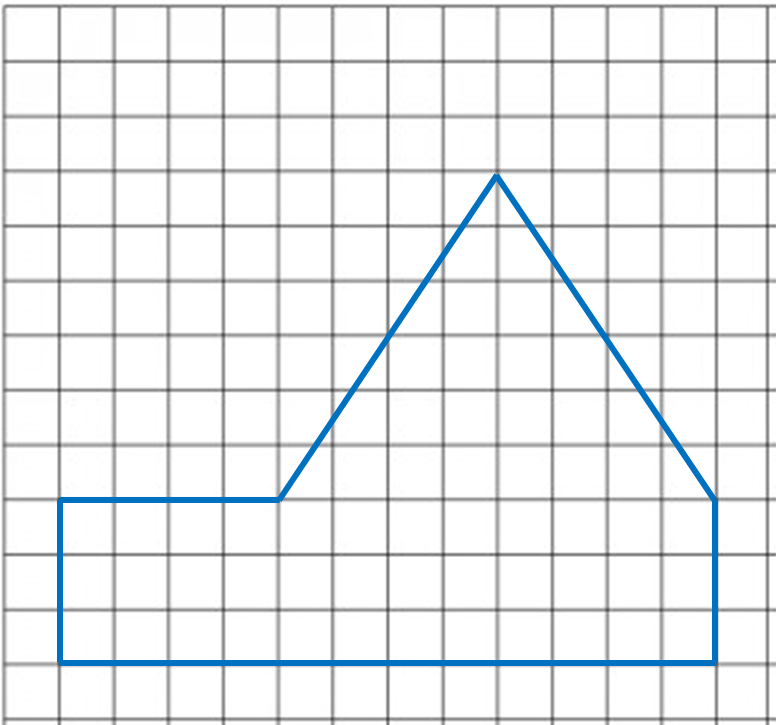
Diagram 6.1 shows a polygon.

(a) If the polygon is redrawn using the scale 1 : 500, calculate the length of side drawn for the side 15 m.
(b) On the square grids in the answer space, redraw the polygon using the scale 1 : 500. The grid has equal squares with sides of 1 cm.
Solution:
(a)
(b)

Question 6 (c):
Diagram 6.3 shows a solid cuboid and a solid cube. The base of the cuboid is a square with sides 9 cm.
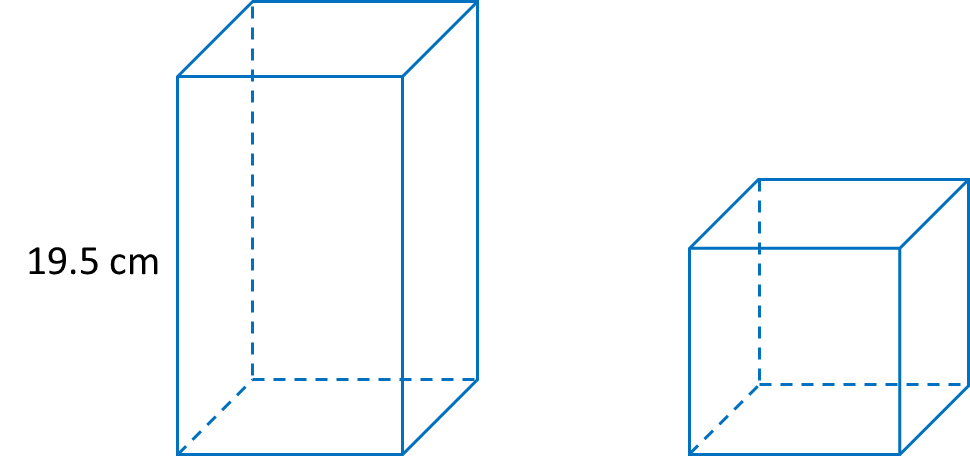
The total surface of area of the cuboid and the cube are equal.
Calculate the length of the side of the cube.
Solution:
Diagram 6.3 shows a solid cuboid and a solid cube. The base of the cuboid is a square with sides 9 cm.

The total surface of area of the cuboid and the cube are equal.
Calculate the length of the side of the cube.
Solution: