13.2.1 Pythagoras’ Theorem, PT3 Focus Practice
Question 1:
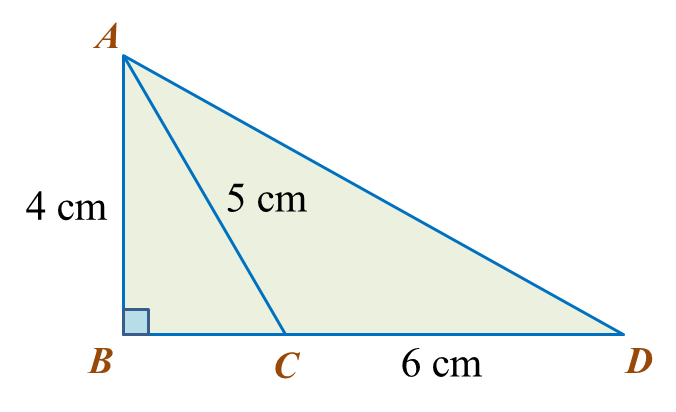
In the diagram, ABC is a right-angled triangle and BCD is a straight line. Calculate the length of AD, correct to two decimal places.
Solution:
In ∆ ABC,
BC2 = 52 – 42
= 25 – 16
= 9
BC = √9
= 3 cm
In ∆ ABD,
BD = BC + CD
= 3 + 6
= 9
AD2 = 42 + 92
= 16 + 81
= 97
AD = √97
= 9.849
= 9.85 cm
Question 2:
Diagram below shows a triangle ACD and ABC is a straight line.
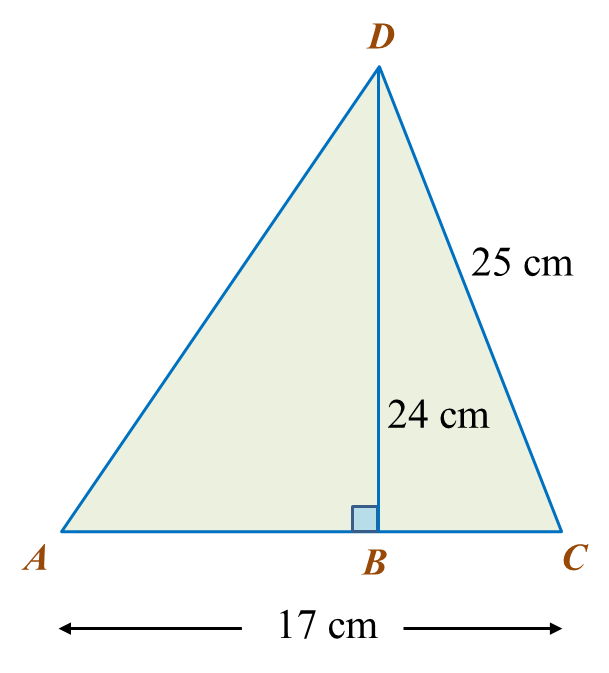
Calculate the length, in cm, of AD.
Solution:
In ∆ DBC,
BC2 = 252 – 242
= 625 – 576
= 49
BC = √49
= 7 cm
AB = 17 – 7 = 10 cm
In ∆ DAB,
AD2 = 102 + 242
= 100 + 576
= 676
AD = √676
= 26 cm