8.1 Lines and Angles
Identifying Parallel, Transversals, Corresponding Angles, Alternate Angles and Interior Angles
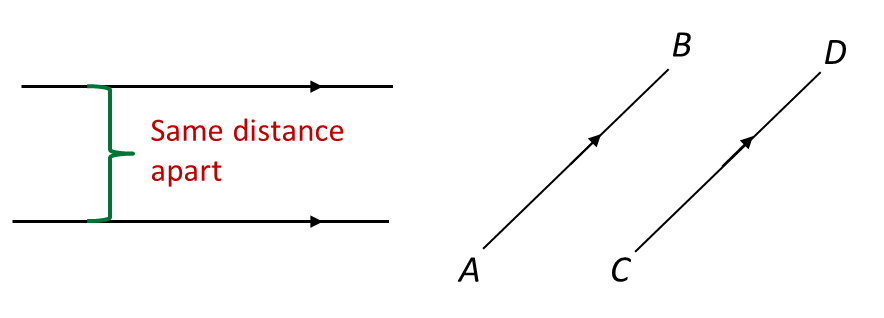
(A) Parallel lines
Parallel lines are lines with the same direction. They remain the same distance apart and never meet.

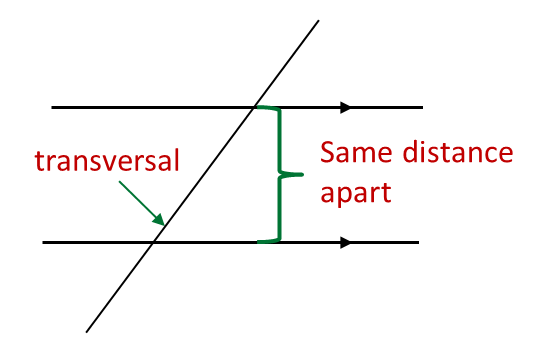
(B) Transversal lines
A transversal is a straight line that intersects two or more straight lines.

(C) Alternate angles
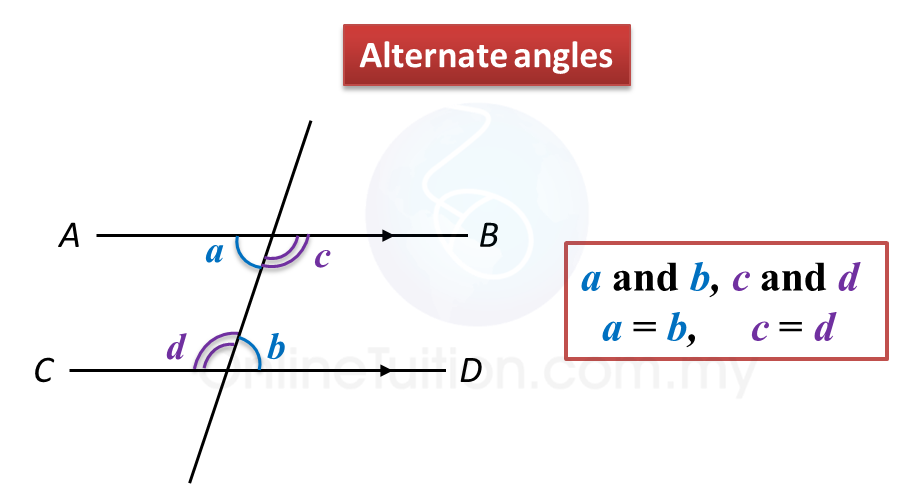
(D) Corresponding angles

(E) Interior angles
