5.2.6 Circles, PT3 Focus Practice

Question 14:
In the Diagram, OKLM is a sector of a circle and OAB is a quadrant of a circle with common centre O.


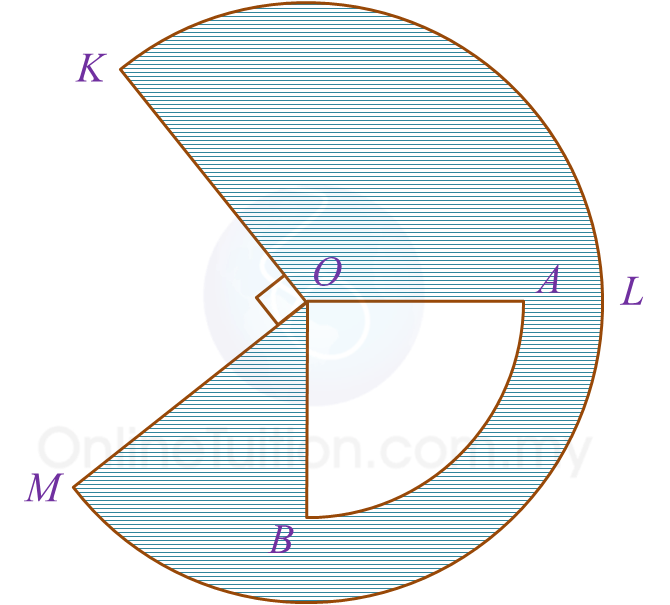
It is given that OA = 8 cm, ∠KOM = 90^o and OK : OB = 3 : 2.
Using  $$ π= 22 7 , calculate
(a) the area, in cm², of the shaded region,
(b) the perimeter, in cm, of the shaded region.


Solution:
(a)
$$ OB=OA=8 cm and OK:OB=3:2 OK OB = 3 2 OK 8 = 3 2 OK= 3 2 ×8 OK=12 Area of the shaded region =( 270 o 360 o × 22 7 × 12 2 )−( 90 o 360 o × 22 7 × 8 2 ) =339 3 7 −50 2 7 =289 1 7  cm 2


(b)
$$ Length of arc KLM = 270 o 360 o ×2× 22 7 ×12 =56 4 7  cm Length of arc AB = 90 o 360 o ×2× 22 7 ×8 =12 4 7  cm Perimeter of shaded region =Length of arc KLM+Length of  arc AB+MO+OK+OA+OB =56 4 7 +12 4 7 +12+12+8+8 =109 1 7  cm

Question 15:
Diagram shows sectors OABC and ODE with the common centre O respectively.


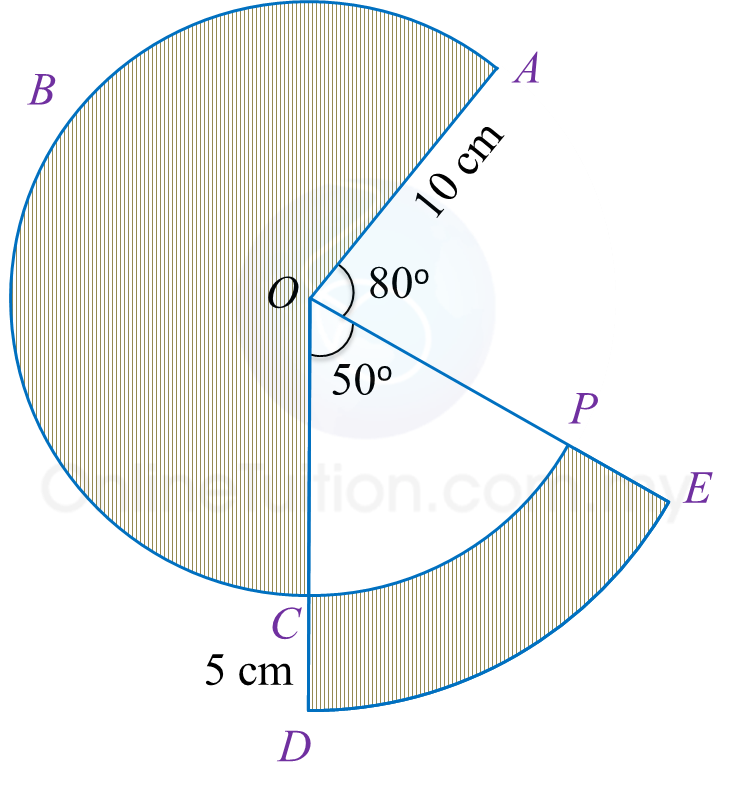
Calculate
(a) the perimeter, in cm, of the whole diagram,
(b) the area, in cm², of the shaded region.

Solution:
(a)
$\begin{array}{l}\text{Perimeter of the whole diagram}\\ =OP+PE+\text{Arc }DE+DC\\ +\text{Arc }CBA+AO\\ =10+5+\left(\frac{{50}^o}{{360}^o}\times 2\times \frac{22}{7}\times 15\right)+5\\ +\left(\frac{{230}^o}{{360}^o}\times 2\times \frac{22}{7}\times 10\right)+10\\ =30+\frac{275}{21}+\frac{2530}{63}\\ =\frac{5245}{63}\\ =83.254\text{ cm}\end{array}$


(b)
$\begin{array}{l}\text{Area of the shaded region}\\ =\left(\frac{{230}^o}{{360}^o}\times \frac{22}{7}\times {10}^2\right)\\ +\left[\left(\frac{{50}^o}{{360}^o}\times \frac{22}{7}\times {15}^2\right)-\left(\frac{{50}^o}{{360}^o}\times \frac{22}{7}\times {10}^2\right)\right]\\ =\frac{12650}{63}+\left(\frac{1375}{14}-\frac{2750}{63}\right)\\ =\frac{3575}{14}\\ =255.36{\text{ cm}}^2\end{array}$