5.2.3 Circles, PT3 Focus Practice

Question 7:
In diagram below, ABC is a semicircle with centre O.

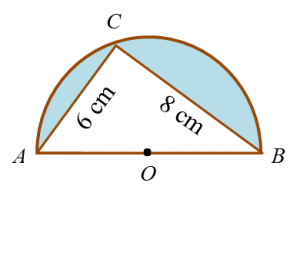Calculate the area, in cm² , of the shaded region.
$\left(\text{Use }\pi =\frac{22}{7}\right)$

Solution:
$\begin{array}{l}\angle ACB={90}^o\\ AB=\sqrt{6^2+8^2}\\ =\sqrt{100}\\ =10\text{ cm}\\ \text{Radius}=10÷2\\ =5\text{ cm}\\ \\ \text{The shaded region}\\ =\left(\frac{1}{2}\times \frac{22}{7}\times 5\times 5\right)-\left(\frac{1}{2}\times 6\times 8\right)\\ =39\frac{2}{7}-24\\ =15\frac{2}{7}{\text{ cm}}^2\end{array}$

Question 8:
In diagram below, ABC is an arc of a circle centre O


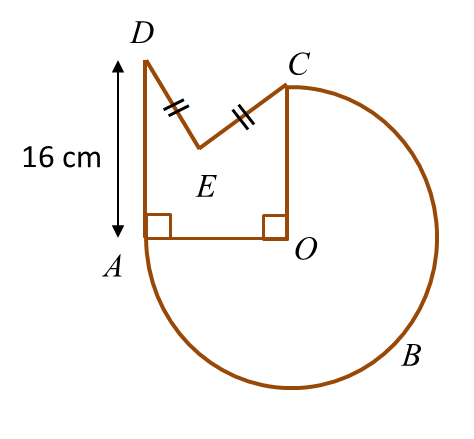
The radius of the circle is 14 cm and AD = 2 DE.
Calculate the perimeter, in cm, of the whole diagram.
$\left(\text{Use }\pi =\frac{22}{7}\right)$

Solution:
$\begin{array}{l}\text{Length of arc }ABC\\ =\frac{3}{4}\times 2\pi r\\ =\frac{3}{4}\times 2\times \frac{22}{7}\times 14\\ =66\text{ cm}\\ \\ \text{Perimeter of the whole diagram}\\ =16+8+8+66\\ =98\text{ cm}\end{array}$

Question 9:
In diagram below, KLMN is a square and KLON is a quadrant of a circle with centre K.


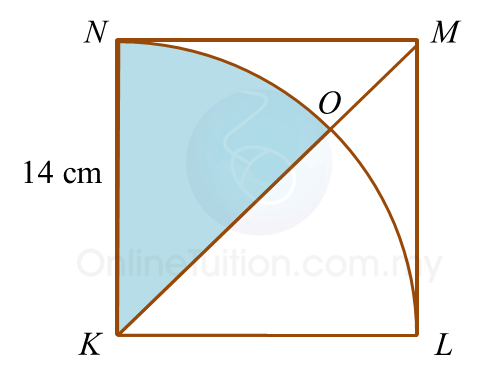
Calculate the area, in cm², of the coloured region.
$\left(\text{Use }\pi =\frac{22}{7}\right)$

Solution:
$\begin{array}{l}\text{Area of the coloured region}\\ =\frac{{45}^o}{{360}^o}\times \pi r^2\\ =\frac{{45}^o}{{360}^o}\times \frac{22}{7}\times {14}^2\\ =77{\text{ cm}}^{\text{2}}\end{array}$