5.2.2 Circles, PT3 Focus Practice - Mathematics

Question 4:

Diagram below shows two sectors. ABCD is a quadrant and BED is an arc of a circle with centre C.

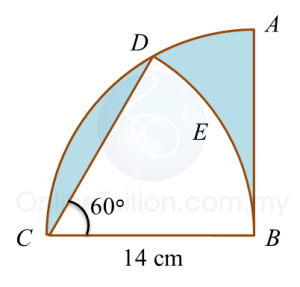
Calculate the area of the shaded region, in cm².

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} The area of sector C B E D \\ = \frac{60^{o}}{360^{o}} \times π r^{2} \\ = \frac{60^{o}}{360^{o}} \times \frac{22}{7} \times 14^{2} \\ = 102 \frac{2}{3} {cm}^{2} \end{array}

\begin{array}{l} The area of quadrant A B C D \\ = \frac{1}{4} \times π r^{2} \\ = \frac{1}{4} \times \frac{22}{7} \times 14^{2} \\ = 154 {cm}^{2} \end{array}

\begin{array}{l} Area of the shaded region \\ = 154 - 102 \frac{2}{3} \\ = 51 \frac{1}{3} {cm}^{2} \end{array}

Question 5:

Diagram below shows a square KLMN. KPN is a semicircle with centre O.

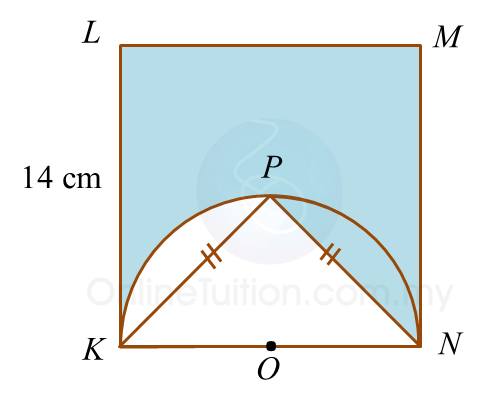
Calculate the perimeter, in cm, of the shaded region.

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} K O = O N = O P = 7 cm \\ P N = \sqrt{7^{2} + 7^{2}} \\ = \sqrt{98} \\ = 9.90 cm \\ Arc length K P \\ = \frac{1}{4} \times 2 \times \frac{22}{7} \times 7 \\ = 11 cm \end{array}

Perimeter of the shaded region

= KL + LM + MN + NP + Arc length PK

= 14 + 14 +14 + 9.90 + 11

= 62.90 cm

Question 6:
In the diagram below, CD is an arc of a circle with centre O.

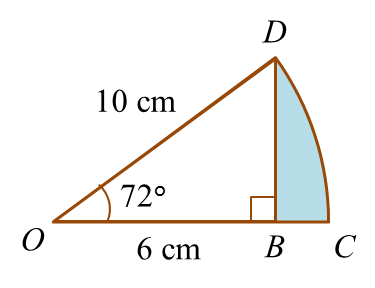
Determine the area of the shaded region.

(Use π = \frac{22}{7})

Solution:

\begin{array}{l} Area of sector = Area of circle \times \frac{72^{o}}{360^{o}} \\ = \frac{22}{7} \times {(10)}^{2} \times \frac{72^{o}}{360^{o}} \\ = \frac{440}{7} {cm}^{2} \\ Area of Δ O B D = \frac{1}{2} \times 6 \times 8 \\ = 24 {cm}^{2} \\ Area of shaded region = \frac{440}{7} - 24 \\ = 38 \frac{6}{7} {cm}^{2} \end{array}