5.2.7 Circles, PT3 Focus Practice

Question 16:
(a) Diagram 16.1 shows a Ferris wheel. The distance between point L and point M is 18 m.

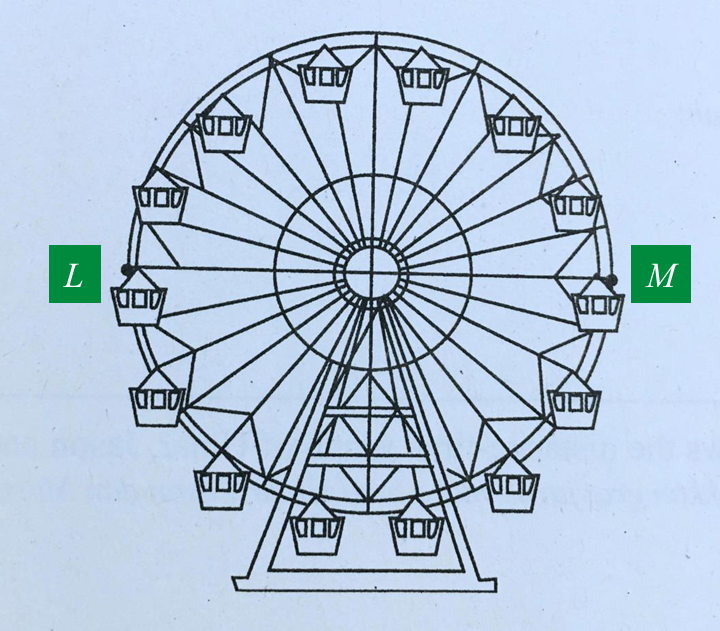Diagram 16.1

Calculate the minimum number of complete spins required to cover the distance of 600 m in a circular motion.


(b) Diagram 16.2 shows one large pizza and two small pizzas. Assume all pizzas are circular with a flat surface.

Diagram 16.2

Using  $\pi =\frac{22}{7}$ , calculate the portion of the large pizza which equals to two small pizzas.


Solution:
(a)
$\begin{array}{l}\text{Diameter}=18\text{ m}\\ \text{Radius}=9\text{ m}\\ \text{Circumference}=2\pi r\\ =2\times \frac{22}{7}\times 9\text{ m}\\ =\frac{396}{7}\text{ m}\\ \frac{396}{7}\times \text{rounds}\left(P\right)=600\text{ m}\\ P=600\times \frac{7}{396}\\ P=\frac{350}{33}\text{ rounds}\\ P=10\frac{20}{33}\\ \\ \text{Thus, the minimum number of}\\ \text{complete spins required}=10.\end{array}$


(b)
$\begin{array}{l}\text{Radius of large pizza}=14\text{ cm}\\ \text{Area of large pizza }\\ =\pi r^2\\ =\frac{22}{7}\times {\left(14\text{ cm}\right)}^2\\ =\frac{22}{7}\times 196{\text{ cm}}^2\\ =616{\text{ cm}}^2\\ \\ \text{Radius of small pizza}=7\text{ cm}\\ \text{Area of small pizza}\\ =\pi r^2\\ =\frac{22}{7}\times {\left(\text{7 cm}\right)}^2\\ =\frac{22}{7}\times 49{\text{ cm}}^2\\ =154{\text{ cm}}^2\\ \\ \text{Area of 2 small pizza}\\ =2\times 154{\text{ cm}}^2\\ =308{\text{ cm}}^2\\ \\ \text{Ratio of area of 1 large pizza :}\\ \text{2 small pizza}\\ 616\text{ : }308\\ \frac{616}{2}\text{ : }308\\ 308\text{ : }308\\ \\ \text{Thus, }\frac{1}{2}\text{large pizza}=\text{2 small pizza}\end{array}$