Question 8 (a):
Diagram 8.1 shows the pattern for a sequence consists of a few buttons.

(i) Based on the amount of buttons in Diagram 8.1, find the fourth and fifth terms of the pattern.
(ii) Hence, write the number of buttons for eighth term.
Solution:
(i)
Fourth term = 4 + 3 + 3 + 3 = 13
Fifth term = 4 + 3 + 3 + 3 + 3 = 16
(ii)
Eight term
= Fifth term + 9
= 16 + 9 = 25
Diagram 8.1 shows the pattern for a sequence consists of a few buttons.

(i) Based on the amount of buttons in Diagram 8.1, find the fourth and fifth terms of the pattern.
(ii) Hence, write the number of buttons for eighth term.
Solution:
(i)
Fourth term = 4 + 3 + 3 + 3 = 13
Fifth term = 4 + 3 + 3 + 3 + 3 = 16
(ii)
Eight term
= Fifth term + 9
= 16 + 9 = 25
Question 8 (b):
(i) Complete Table 8.1 in the answer space for the equation A = x2 + 2x + 3 by writing down the value of A, when x = 3.
Answer:

(ii) For this part of the equation, use the graph paper provided on the next page. You may use a flexible curve rule.
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of A = x2 + 2x + 3 for 0 ≤ x ≤ 5.
Solution:
(i)
x = 3
A = 32 + 2(3) + 3
= 9 + 6 + 3
= 18
(ii)
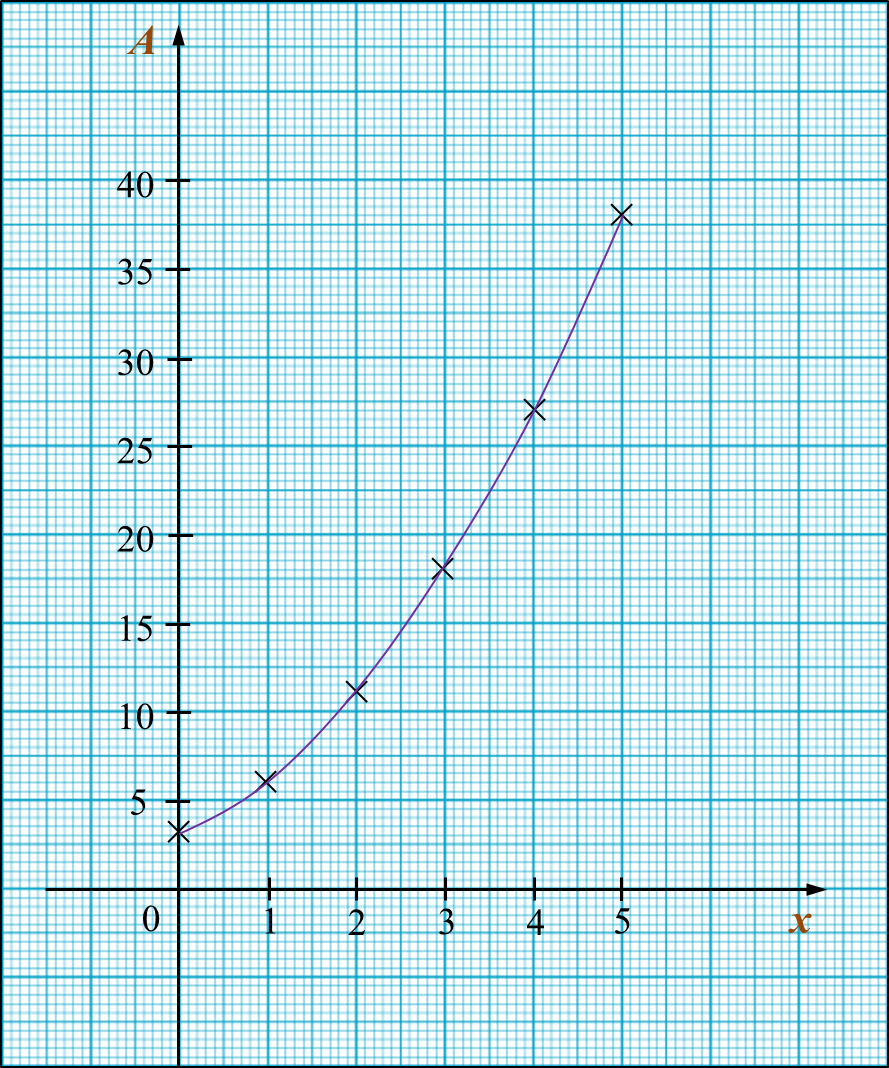
(i) Complete Table 8.1 in the answer space for the equation A = x2 + 2x + 3 by writing down the value of A, when x = 3.
Answer:

(ii) For this part of the equation, use the graph paper provided on the next page. You may use a flexible curve rule.
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of A = x2 + 2x + 3 for 0 ≤ x ≤ 5.
Solution:
(i)
x = 3
A = 32 + 2(3) + 3
= 9 + 6 + 3
= 18
(ii)

Question 8 (c):
Diagram 8.2 shows the offer of services by a telecommunication company.

(i) In a particular month, the total payment is H. If x of SMS were sent and y minutes of phone calls were made, express H in terms of x and y.
(ii) In August, Aliah has to pay RM63. If she sent 25 SMS in that month, how many minutes of phone calls made by Aliah?
Solution:
(i)
H = (0.20 × x) + (0.15 × y)
H = 0.2x + 0.15y
(ii)
Diagram 8.2 shows the offer of services by a telecommunication company.

(i) In a particular month, the total payment is H. If x of SMS were sent and y minutes of phone calls were made, express H in terms of x and y.
(ii) In August, Aliah has to pay RM63. If she sent 25 SMS in that month, how many minutes of phone calls made by Aliah?
Solution:
(i)
H = (0.20 × x) + (0.15 × y)
H = 0.2x + 0.15y
(ii)