9.3.1 Straight Lines, PT3 Focus Practice - Mathematics

Question 1:

In diagram below, ABCD is a trapezium drawn on a Cartesian plane. BC is parallel to AD and O is the origin. The equation of the straight line BC is 3y = kx+ 7 and the equation of the straight line AD is

y = \frac{1}{2} x + 3

$y = \frac{1}{2} x + 3$

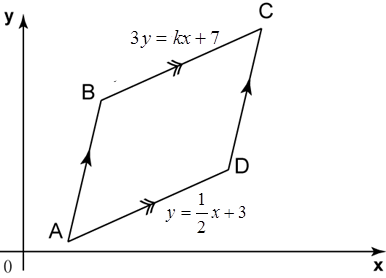
Find

(a) the value of k,

(b) the x-intercept of the straight line BC.

Solution:
(a)

Equation of BC :

3y = kx + 7

\begin{matrix} y = \frac{k}{3} x + \frac{7}{3} ∴ Gradient of B C = \frac{k}{3} Equation of A D : y = \frac{1}{2} x + 3 ∴ Gradient of A D = \frac{1}{2} Gradient of B C = gradient of A D \frac{k}{3} = \frac{1}{2} ∴ k = \frac{3}{2} \end{matrix}

$\begin{array}{l} y = \frac{k}{3} x + \frac{7}{3} \\ ∴ Gradient of B C = \frac{k}{3} \\ Equation of A D : y = \frac{1}{2} x + 3 \\ ∴ Gradient of A D = \frac{1}{2} \\ Gradient of B C = gradient of A D \\ \frac{k}{3} = \frac{1}{2} \\ ∴ k = \frac{3}{2} \end{array}$

Gradient of BC = gradient of AD

\begin{matrix} \frac{k}{3} = \frac{1}{2} ∴ k = \frac{3}{2} \end{matrix}

$\begin{array}{l} \frac{k}{3} = \frac{1}{2} \\ ∴ k = \frac{3}{2} \end{array}$

(b)
Equation of BC,

3 y = \frac{3}{2} x + 7

$3 y = \frac{3}{2} x + 7$

For x-intercept, y = 0

\begin{matrix} 3 (0) = \frac{3}{2} x + 7 \frac{3}{2} x = - 7 x = - \frac{14}{3} \end{matrix}

$\begin{array}{l} 3 (0) = \frac{3}{2} x + 7 \\ \frac{3}{2} x = - 7 \\ x = - \frac{14}{3} \end{array}$

Therefore x-intercept of BC =

- \frac{14}{3}

$- \frac{14}{3}$

Question 2:

In diagram below, O is the origin. Straight line MN is parallel to a straight line OK.

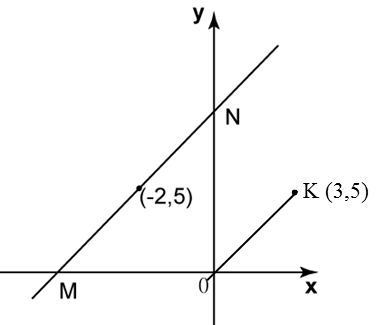
Find

(a) the equation of the straight line MN,

(b) the x-intercept of the straight line MN.

Solution:

(a)
Gradient of MN = gradient of OK

Gradient of MN

\begin{matrix} = \frac{5 - 0}{3 - 0} = \frac{5}{3} \end{matrix}

$\begin{array}{l} = \frac{5 - 0}{3 - 0} \\ = \frac{5}{3} \end{array}$

Substitute m = 5/3 and (–2, 5) into y = mx + c

5 = \frac{5}{3} (- 2) + c

$5 = \frac{5}{3} (- 2) + c$

15 = – 10 + 3c

3c = 25

c = 25/3

Therefore equation of MN:

y = \frac{5}{3} x + \frac{25}{3}

$y = \frac{5}{3} x + \frac{25}{3}$

(b)

For x-intercept, y = 0

\begin{matrix} 0 = \frac{5}{3} x + \frac{25}{3} \frac{5}{3} x = - \frac{25}{3} \end{matrix}

$\begin{array}{l} 0 = \frac{5}{3} x + \frac{25}{3} \\ \frac{5}{3} x = - \frac{25}{3} \end{array}$

5x = –25

x = –5

Therefore x-intercept of MN = –5

Leave a Comment Cancel reply