5.2.3 Coordinates, PT3 Focus Practice - Mathematics

Question 7:

Diagram shows a straight line PQ on a Cartesian plane.

Calculate the length, in unit, of PQ.

Solution:

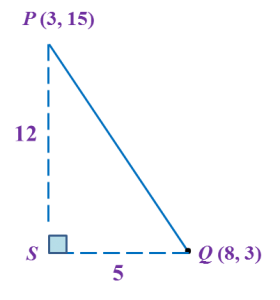PS = 15 – 3 = 12 units

SQ = 8 – 3 = 5 units

By Pythagoras’ theorem,

PQ²= PS² + SQ²

= 12²+ 5²

PQ = √169

= 13 units

Question 8:

The diagram shows an isosceles triangle STU.

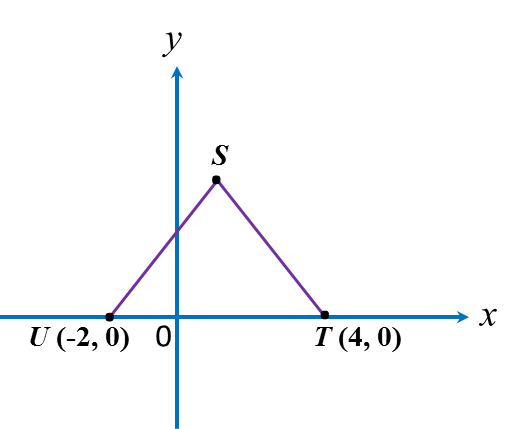
Given that ST = 5 units, the coordinates of point S are

Solution:

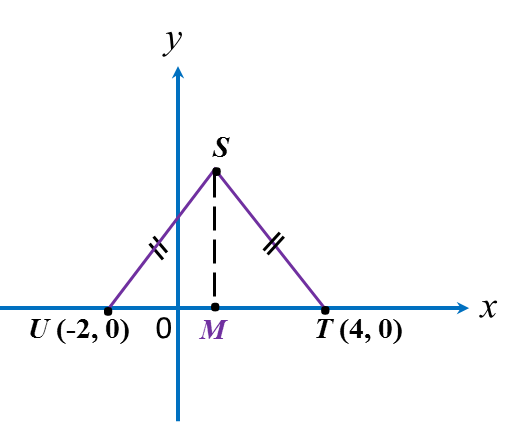
For an isosceles triangle STU, M is the midpoint of straight line TU.

\begin{array}{l} x - coordinate of M \\ = \frac{- 2 + 4}{2} = 1 \end{array}

Point M = (1, 0)

MT = 4 – 1 = 3 units

By Pythagoras’ theorem,

SM²= ST² – MT²

= 5² – 3²

= 25 – 9

= 16

SM = √16

= 4

Therefore, point S = (1, 4).