7.1.2 Scales for the Coordinate Axes
1. The scale for an axis is the number of units represented by a specific length along the axes.
2. The scale on a coordinate is usually written in the form of a ratio.
Example:
A scale of 1 : 2 means one unit on the graph represents 2 units of the actual length.
3. Both coordinate axes on the Cartesian plane may have
(a) the same scales, or
(b) different scales.
Example:
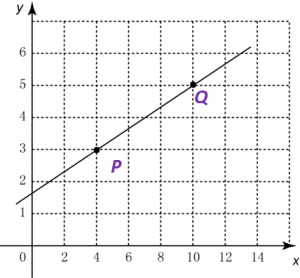
1 unit on the x-axis represents 2 units.
1 unit on the y-axis represents 1 unit.
Therefore the scale for x-axis is 1 : 2 and the scale for y-axis is 1 : 1.
Coordinates of:
P (4, 3) and Q (10, 5).7.1.3 Distance between Two Points
1. Finding the distance between two points on a Cartesian plane is the same as finding the length of the straight line joining them.
2. The distance between two points can be calculated by using Pythagoras’ theorem.
Example:
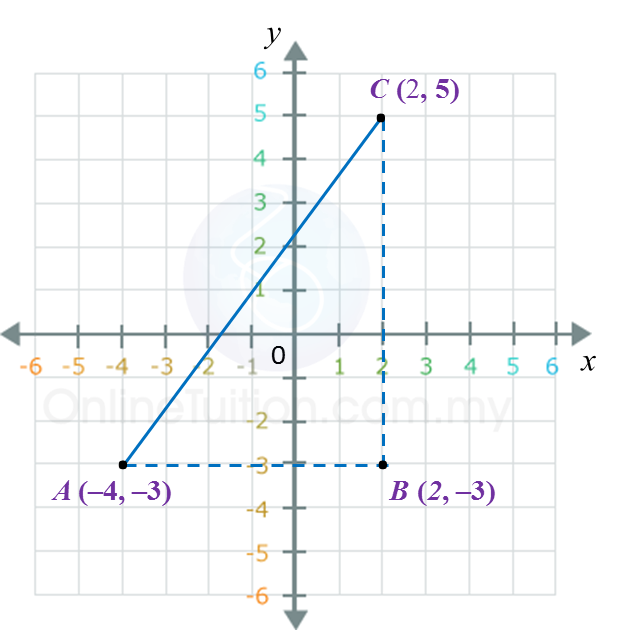
AB = 2 – (–4) = 2 + 4 = 6 units
BC = 5 – (–3) = 5 + 3 = 8 units
By Pythagoras’ theorem,
AC2 = AB2 + AC2
= 62 + 82
AC = √100
= 10 units
3. Distance is always a positive value.
7.1.4 Midpoint
The midpoint of a straight line joining two points is the middle point that divides the straight line into two equal halves.
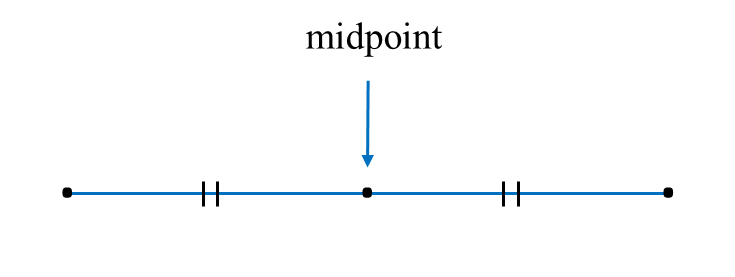

Example:
The coordinate of the midpoint of (7, –5) and (–3, 11) are