4.2.2 Polygons, PT3 Practice - Mathematics

Question 4:

In the diagram below, KLMNP is a regular pentagon. LKS and MNQ are straight lines.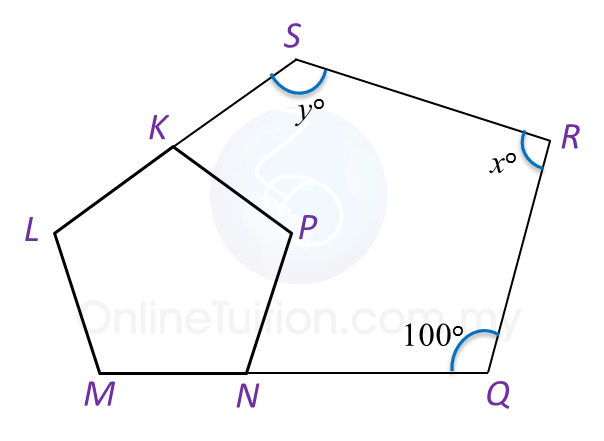

Find the value of x + y.

Solution:

\begin{array}{l} Size of each interior angle of a regular pentagon \\ = \frac{(5 - 2) \times 180^{o}}{5} \\ = 108^{o} \\ ∠ P K S = ∠ P N Q = 180^{o} - 108^{o} = 72^{o} \\ Reflex angle ∠ K P N = 360^{o} - 108^{o} = 252^{o} \end{array}

\begin{array}{l} Sum of interior angles of a hexagon \\ = (6 - 2) \times 180^{o} \\ = 720^{o} \\ ∴ x^{o} + y^{o} + 72^{o} + 252^{o} + 72^{o} + 100^{o} = 720^{o} \\ x^{o} + y^{o} = 720^{o} - 496^{o} \\ = 224^{o} \\ x + y = 224 \end{array}

Question 5:

In Diagram below, PQR is an isosceles triangle and PRU is a straight line.

Find the value of x + y.

Solution:

\begin{array}{l} x^{o} = 180^{o} - 20^{o} - 20^{o} = 140^{o} \\ ∠ P R S = 180^{o} - 110^{o} = 70^{o} \\ y^{o} + 85^{o} + 75^{o} + 70^{o} = 360^{o} \\ y^{o} + 230^{o} = 360^{o} \\ y^{o} = 130^{o} \\ x^{o} + y^{o} = 140^{o} + 130^{o} \\ = 270^{o} \\ x + y = 270 \end{array}

Question 6:
In diagram below, PQRSTU is a regular hexagon QUV is a straight line.

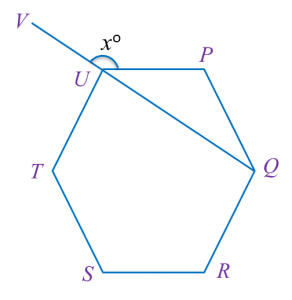
Find the value of x.

Solution:

\begin{array}{l} Each interior angle \\ = \frac{(6 - 2) \times 180^{o}}{6} \\ = 120^{o} \\ ∠ P U Q = \frac{180^{o} - 120^{o}}{2} = 30^{o} (△ P U Q is a isosceles triangle) \\ x^{o} = 180^{o} - 30^{o} \\ = 150^{o} \\ x = 150 \end{array}