Question 5:
Diagram below shows a Venn diagram with the number of elements of set P, set Q and set R.
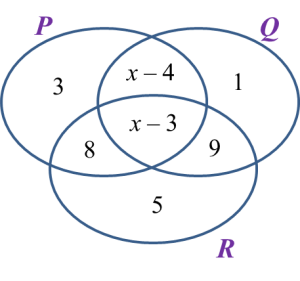

It is given that the universal set,
Find the value of x.
Solution:
n(Q)’ = n(Q ∩ R)
3 + 8 + 5 = x– 3 + 9
16 = x + 6
x = 10
Question 6:
Diagram below is a Venn diagram showing the number of quiz participants in set P, set Q and set R.
It is given that the universal set,
, set P = {Science quiz participants}, set Q = {Mathematics quiz participants} and set R = {History quiz participants}.
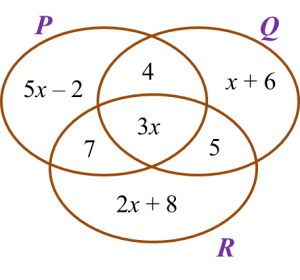
If the number of participants who participate in only one quiz is 76, find the total number of the participants.
Solution:
Number of participants who participate in only one quiz = 76
(5x – 2) + (x + 6) + (2x + 8) = 76
8x + 12 = 76
8x = 64
x = 8
8x = 64
x = 8
Total number of the participants
= 76 + 7 + 4 + 5 + 3(8)
= 116Question 7:
Diagram below is a Venn diagram showing the number of students in set K, set L and set M.
It is given that the universal set,
, set K = {Karate Club}, set L = {Life Guards Club} and set M = {Martial Arts Club}.
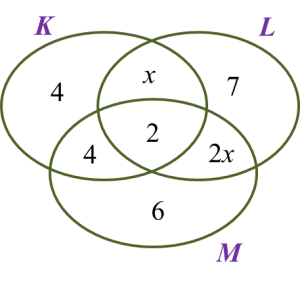

If the number of students who join both the Life Guards Club and the Martial Arts Club is 8, find the number of students who join only two clubs.
Solution:
Number of students who join both the Life Guards Club and the Martial Arts Club = n(L ∩ M) = 2 + 2x
2 + 2x = 8
2x = 6
x = 3
Number of students who join only two clubs
= x + 4 + 2x
= 3 + 4 + 2(3)
= 13