8.2.1 Lines and Angles, PT3 Practice - Mathematics

8.2.1 Lines and Angles, PT3 Practice

Question 1:

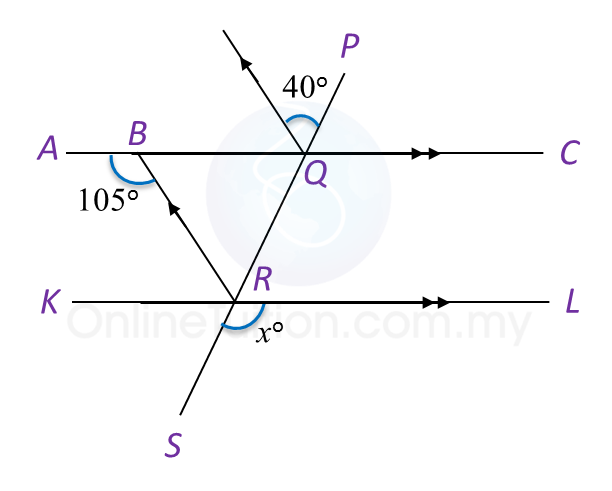
In Diagram below, PQRS, ABQC and KRL are straight lines.

Find the value of x.

Solution:

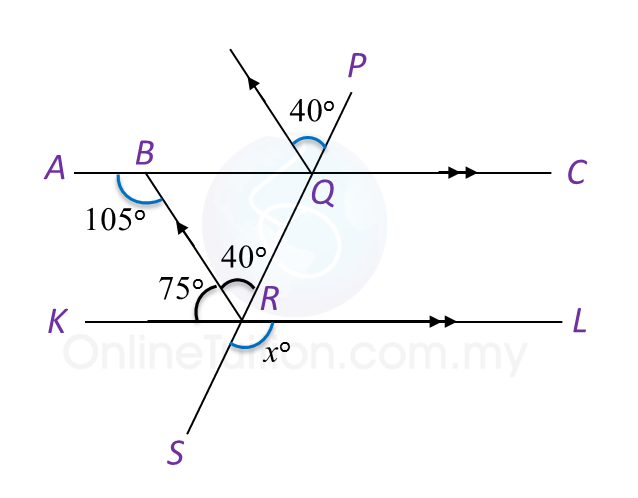
\begin{array}{l} ∠ K R B + ∠ A B R = 180^{o} \leftarrow Sum of interior angles \\ ∠ K R B + 105^{o} = 180^{o} \\ ∠ K R B = 180^{o} - 105^{o} \\ ∠ K R B = 75^{o} \\ ∠ B R Q = 40^{o} \leftarrow Corresponding angle \\ x^{o} = ∠ S R L = ∠ K R Q \leftarrow \begin{array}{l} Vertically \\ opposite angle \end{array} \\ x^{o} = 75^{o} + 40^{o} \\ = 115^{o} \\ x = 115 \end{array}

Question 2:

(a) In Diagram below, PQR and SQT are straight lines.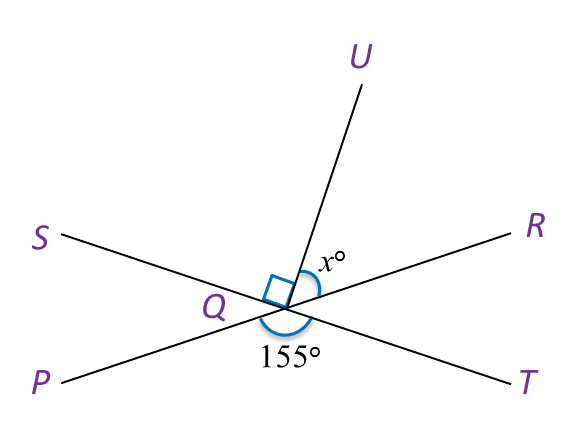

Find the value of x.

(b) In Diagram below, PQRS is a straight line. Find the value of x.

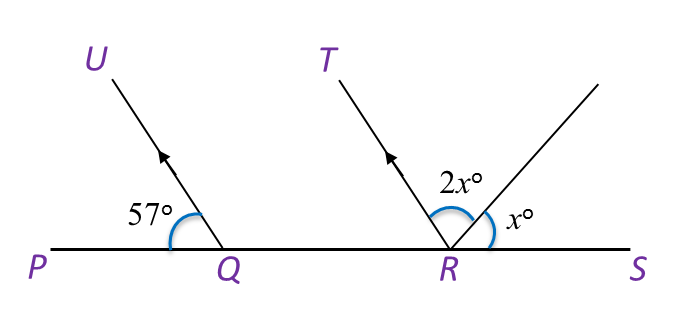
Solution:

(a)

\begin{array}{l} ∠ P Q T = ∠ R Q S \\ x^{o} + 90^{o} = 155^{o} \\ x^{o} = 155^{o} - 90^{o} \\ = 65^{o} \\ x = 65 \end{array}

(b)

\begin{array}{l} ∠ Q R T = 57^{o} \\ x^{o} + 2 x^{o} = 180^{o} - 57^{o} \\ 3 x^{o} = 123^{o} \\ x^{o} = \frac{123^{o}}{3} \\ x^{o} = 41^{o} \\ x = 41 \end{array}

Question 3:
In Diagram below, PQRST is a straight line. Find the value of x.

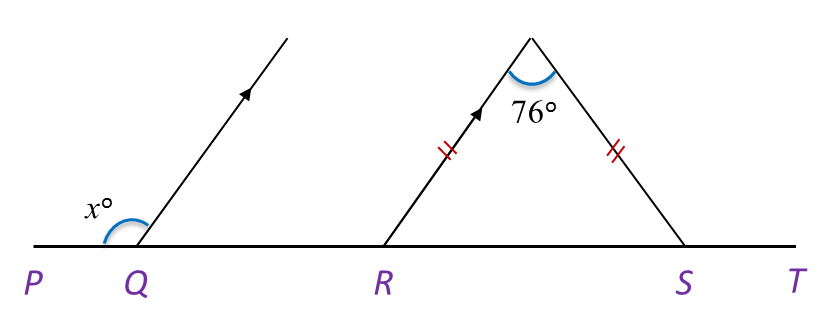
Solution:

\begin{array}{l} Interior angle of R = (180^{o} - 76^{o}) \div 2 = 52^{o} \\ ∠ x = exterior angle of R (corresponding angles) \\ Hence, x = 76^{o} + 52^{o} = 128^{o} \end{array}

Tina

March 5, 2018 at 1:23 pm | Reply

NICE!!!!
aisyah

September 30, 2018 at 1:41 pm | Reply

tq..
SHAHID

September 28, 2019 at 7:02 am | Reply

this is sooooooooooooo useful but it would have been better if you explain