7.1.2 Linear Inequalities - Mathematics

7.1.4 Solve Inequalities in One Variable

To solve linear inequalities in one variable, use inverse operation to make the variable as the subject of the inequality.

Example:

Solve the following linear inequalities.

\begin{array}{l} (a) 3 - 2 x < 1 \\ (b) \frac{5 - 2 x}{3} \leq 7 \end{array}

Solution:

(a)

\begin{array}{l} 3 - 2 x < 1 \\ 3 - 2 x - 3 < 1 - 3 \\ - 2 x < - 2 \\ 2 x > 2 \\ \frac{2 x}{2} > \frac{2}{2} \\ x > 1 \end{array}

(b)

\begin{array}{l} \frac{5 - 2 x}{3} \leq 7 \\ (\frac{5 - 2 x}{3}) \times 3 \leq 7 \times 3 \\ 5 - 2 x \leq 21 \\ - 2 x \leq 16 \\ 2 x \geq - 16 \\ \frac{2 x}{2} \geq - \frac{16}{2} \\ x \geq - 8 \end{array}

7.1.5 Simultaneous Linear Inequalities in One Variable

1. The common values of two simultaneous inequalities are values which satisfy both linear inequalities.

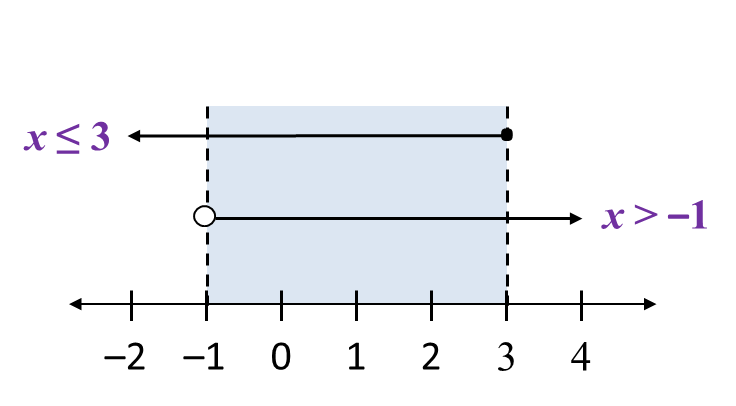
The common values of the simultaneous linear inequalities x ≤ 3 and x > –1 is –1 < x ≤ 3.

2. To solve two simultaneous linear inequalities is to find a single equivalent inequality which satisfies both inequalities.