5.2.2 Trigonometric Ratios, PT3 Focus Practice - Mathematics

Question 4:

In the diagram, PQR and QTS are straight lines.

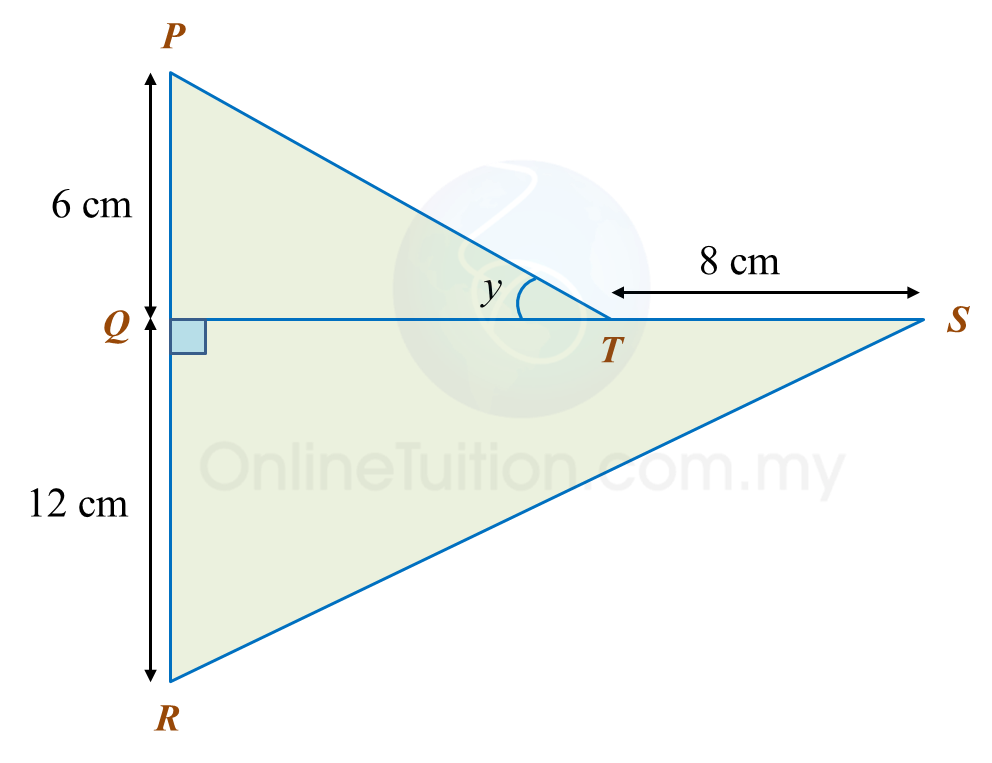
It is given that

tan y = \frac{3}{4}

$\tan y = \frac{3}{4}$ , calculate the length, in cm, of RS.

Solution:

\begin{matrix} In △ P Q T, tan y = \frac{P Q}{Q T} \frac{3}{4} = \frac{6}{Q T} Q T = 6 \times \frac{4}{3} = 8 cm In △ Q R S, Q S = 8 + 8 = 16 cm ∴ R S^{2} = 12^{2} + 16^{2} \leftarrow pythagoras’ Theorem = 144 + 256 = 400 R S = \sqrt{400} = 20 cm \end{matrix}

$\begin{array}{l} In △ P Q T, \\ \tan y = \frac{P Q}{Q T} \\ \frac{3}{4} = \frac{6}{Q T} \\ Q T = 6 \times \frac{4}{3} \\ = 8 cm \\ In △ Q R S, Q S = 8 + 8 = 16 cm \\ ∴ R S^{2} = 12^{2} + 16^{2} \leftarrow pythagoras’ Theorem \\ = 144 + 256 \\ = 400 \\ R S = \sqrt{400} \\ = 20 cm \end{array}$

Question 5:

In the diagram, PQR is a straight line.

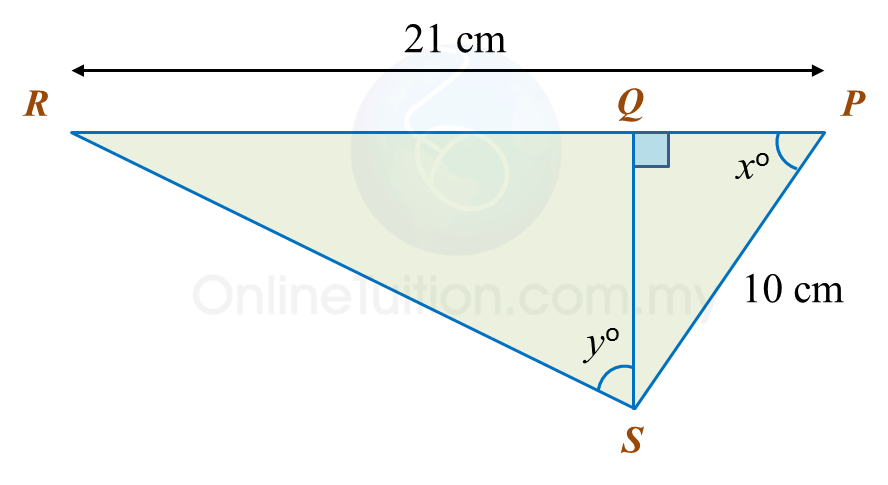
It is given that

cos x^{o} = \frac{3}{5}

$\cos x^{o} = \frac{3}{5}$ , hence sin y^o =

Solution:

\begin{matrix} cos x^{o} = \frac{P Q}{P S} \frac{P Q}{10} = \frac{3}{5} P Q = \frac{3}{5} \times 10 = 6 cm Q R = P R - P Q = 21 - 6 = 15 cm \end{matrix}

$\begin{array}{l} \cos x^{o} = \frac{P Q}{P S} \\ \frac{P Q}{10} = \frac{3}{5} \\ P Q = \frac{3}{5} \times 10 \\ = 6 cm \\ Q R = P R - P Q \\ = 21 - 6 \\ = 15 cm \end{array}$

\begin{matrix} Q S^{2} = 10^{2} - 6^{2} \leftarrow pythagoras' Theorem = 100 - 36 = 64 Q S = \sqrt{64} = 8 cm R S^{2} = 15^{2} + 8^{2} = 225 + 64 = 289 R S = \sqrt{289} = 17 cm sin y^{o} = \frac{15}{17} \end{matrix}

$\begin{array}{l} Q S^{2} = 10^{2} - 6^{2} \leftarrow pythagoras' Theorem \\ = 100 - 36 \\ = 64 \\ Q S = \sqrt{64} \\ = 8 cm \\ R S^{2} = 15^{2} + 8^{2} \\ = 225 + 64 \\ = 289 \\ R S = \sqrt{289} \\ = 17 cm \\ \sin y^{o} = \frac{15}{17} \end{array}$

Question 6:
In diagram below, ABE and DBC are two right-angled triangles ABC and DEB are straight lines.

It is given that cos y^{o} = \frac{3}{5} .

$It is given that \cos y^{o} = \frac{3}{5} .$
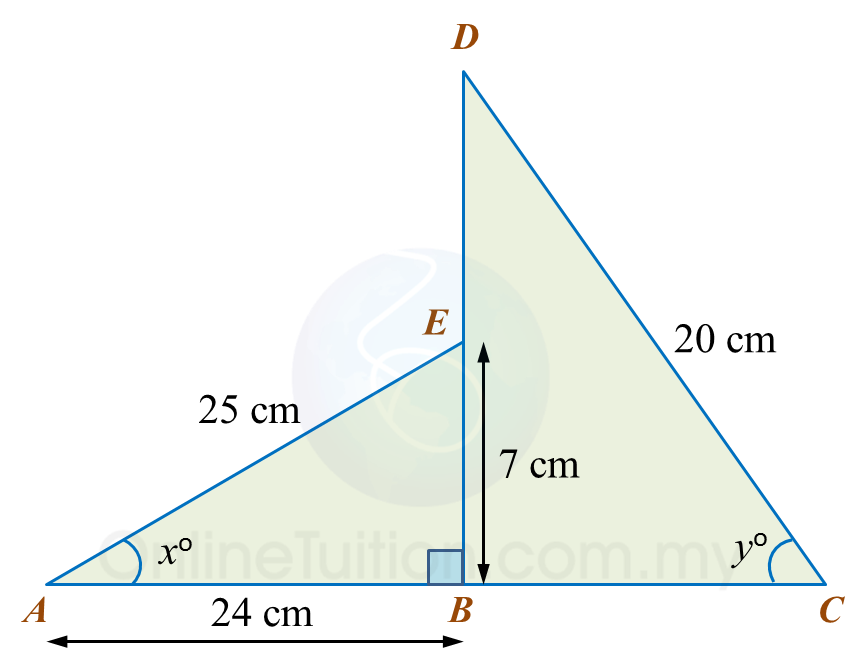
(a) Find the value of tan x^o.
(b) Calculate the length, in cm, of DE.

Solution:

(a) tan x^{o} = \frac{7}{24}

$(a) \tan x^{o} = \frac{7}{24}$

\begin{matrix} (b) cos y^{o} = \frac{B C}{20} \frac{3}{5} = \frac{B C}{20} B C = \frac{3}{5} \times 20 = 12 cm ∴ B D^{2} = 20^{2} - 12^{2} = 400 - 144 = 256 B D = \sqrt{256} = 16 cm D E = 16 - 7 = 9 cm \end{matrix}

$\begin{array}{l} (b) \\ \cos y^{o} = \frac{B C}{20} \\ \frac{3}{5} = \frac{B C}{20} \\ B C = \frac{3}{5} \times 20 \\ = 12 cm \\ ∴ B D^{2} = 20^{2} - 12^{2} \\ = 400 - 144 \\ = 256 \\ B D = \sqrt{256} \\ = 16 cm \\ D E = 16 - 7 \\ = 9 cm \end{array}$

Leave a Comment Cancel reply