5.2.1 Coordinates, PT3 Focus Practice
Question 1:
In diagram below, Q is the midpoint of the straight line PR.
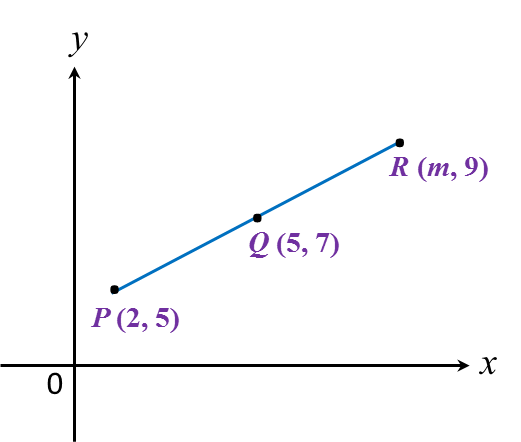
The value of m is
Solution:
Question 2:
In diagram below, P and Q are points on a Cartesian plane.
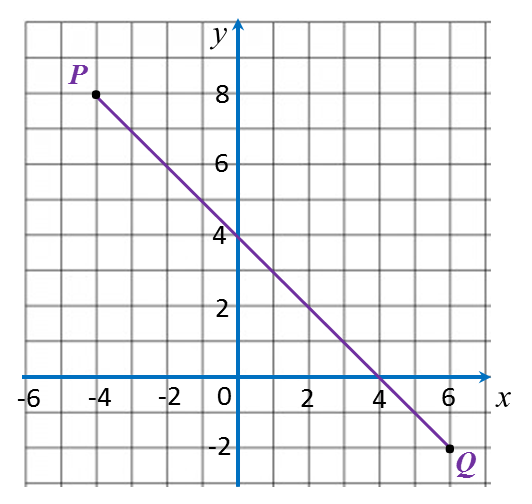
If M is the midpoint of PQ, then the coordinates of M are
Solution:
Question 3:
Find the distance between P (–4, 6) and Q (20, –1).
Solution: