7.2.1 Linear Inequalities, PT3 Focus Practice
Question 1:
Draw a number line to represent the solution for the linear inequalities –3 < 5 – x ≤ 4.
Solution:
–3 < 5 – x and 5 – x ≤ 4
x < 5 + 3 and –x ≤ 4 – 5
x < 8 and –x ≤ –1 → x ≥ 1
Thus, the solution is 1 ≤ x < 8
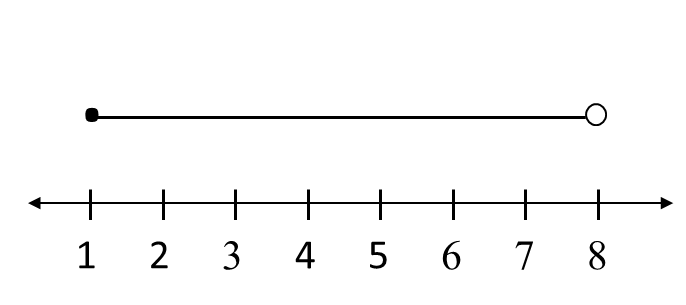
Question 2:
Solve the following simultaneous linear inequalities.
Solution:
3x – 5 ≤ 1
3x ≤ 1 + 5
3x ≤ 6
x ≤ 2
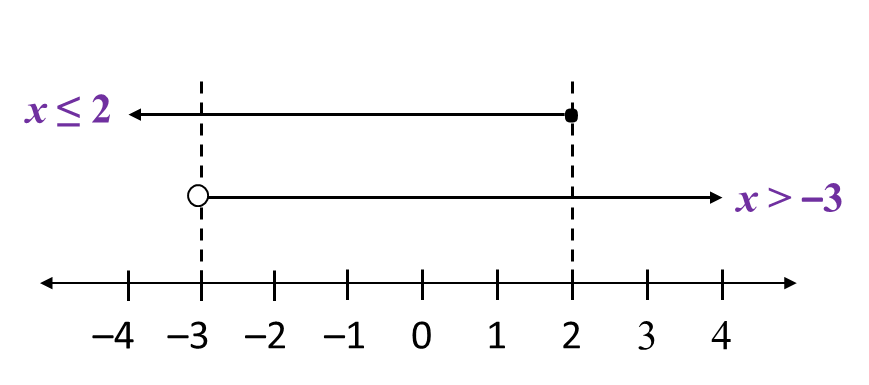
The solution is –3 < x ≤ 2.
Question 3:
The solution for the inequality 2 + x < 3x – 4 is
Solution:
2 + x < 3x – 4
x – 3x < –4 – 2
–2x < –6
–x < –3
x > 3
Question 4:
The solution for the inequality –2 (6y + 3) < 3 (4 – 2y) is
Solution:
–2 (6y + 3) < 3 (4 – 2y)
–12y – 6 < 12 – 6y
–12y + 6y < 12 + 6
–6y < 18
–y < 3
y > –3

