5.2.1 Circles, PT3 Focus Practice
Question 1:
Diagram below shows a circle with centre O.

The radius of the circle is 35 cm.
Calculate the length, in cm, of the major arc AB.
Solution:
Angle of the major arc AB = 360o – 144o= 216o
Question 2:
In diagram below, O is the centre of the circle. SPQ and POQ are straight lines.
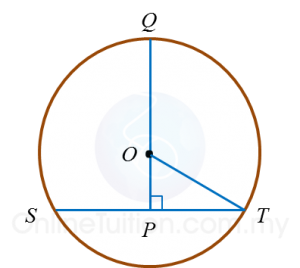
The length of PO is 8 cm and the length of POQ is 18 cm.
Calculate the length, in cm, of SPT.
Solution:
Radius = 18 – 8 = 10 cm
PT2 = 102 – 82
= 100 – 64
= 36
PT = 6 cm
Length of SPT = 6 + 6
= 12 cm
Question 3:
Diagram below shows two circles. The bigger circle has a radius of 14 cm with its centre at O.
The smaller circle passes through O and touches the bigger circle.
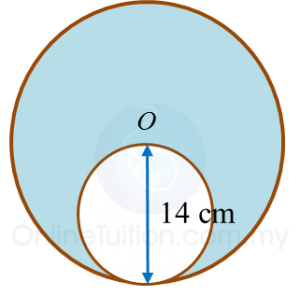
Calculate the area of the shaded region.
Solution:
for question 5, may i know why KO,ON & OP = 7 cm? wasnt it supposed to be 14 cm ?
Thanks for pointing out our mistake.
We had made correction on the Diagram.