4.2.1 Polygons, PT3 Practice
Question 1:
Diagram below shows a pentagon PQRST. TPU and RSV are straight lines.


Find the value of x.
Solution:
Sum of interior angles of a pentagon=(5−2)×180o=3×180o=540o∠TSR=180o−70o =110o∠TPQ=180o−85o =95oxo=540o−(110o+105o+115o+95o)=540o−425o=115o x=115
Question 2:
In Diagram below, PQRSTU is a hexagon. APQ and BTS are straight lines.
Find the value of x + y.
Solution:
∠QPU=180o−160o=20oReflex∠PUT=360o−80o=280o∠UTS=180o−120o=60o∠TSR=180o−35o=145oSum of interior angles of a hexagon=(6−2)×180o=720oxo+yo+145o+60o+280o+20o=720oxo+yo=720o−505o=215ox+y=215
Question 3:
Diagram below shows a regular hexagon PQRSTU. PUV is a straight line.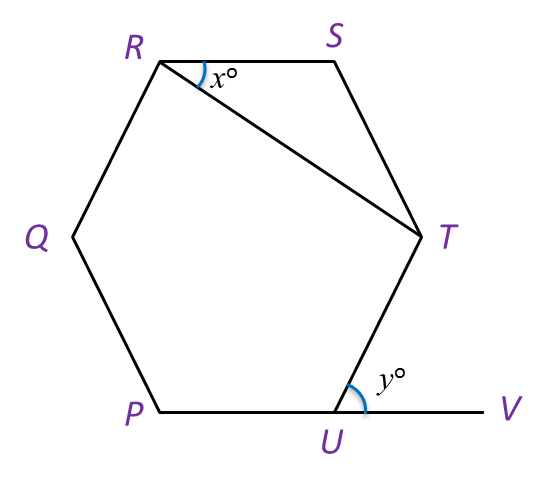
Find the value of x + y.
Solution:
Size of each interior angle of a regular hexagon=(6−2)×180o6=120oxo=180o−120o2=30oyo=180o−120o=60oxo+yo=30o+60o=90ox+y=90
answer in Question 1 is error. The answer is 115.
Thanks for pointing out our mistake.
We had done the correction accordingly.
I like these questions .