8.2.2 Loci in Two Dimensions, PT3 Focus Practice
Question 3:
Diagram below in the answer space shows a quadrilateral ABCD drawn on a grid of equal squares with sides of 1 unit.
X, Y and Z are three moving points inside the quadrilateral ABCD.
(a) X is the point which moves such that it is always equidistant from point B and point D.
By using the letters in diagram, state the locus of X.
(b) On the diagram, draw,
(i) the locus of the point Y such that it is always 6 units from point A,
(ii) the locus of the point Z which moves such that its distance is constantly 3 units from the
line AB.
(i) the locus of the point Y such that it is always 6 units from point A,
(ii) the locus of the point Z which moves such that its distance is constantly 3 units from the
line AB.
(c) Hence, mark with the symbol ⊗ the intersection of the locus of Y and the locus of Z.
Answer:
(b)(i),(ii) and (c)
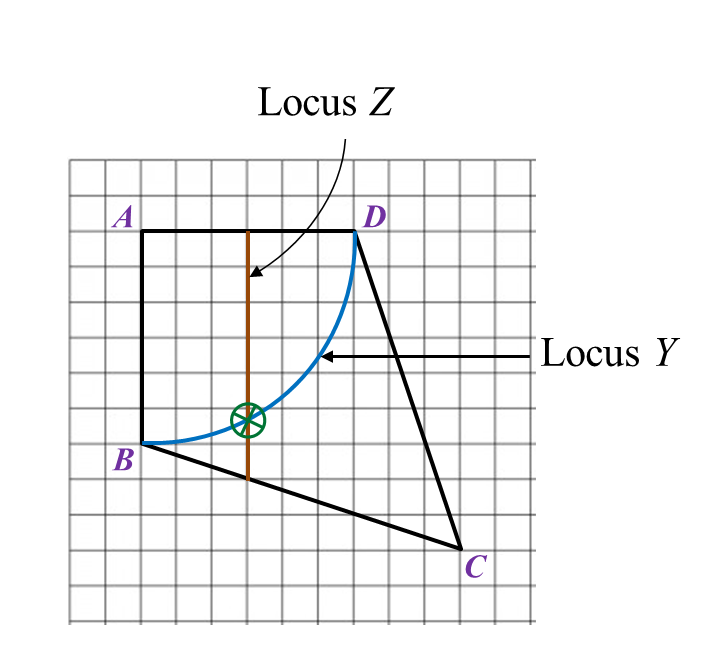
Solution:
(a) The locus of X is the line AC.
(b)(i),(ii) and (c)
Question 4:
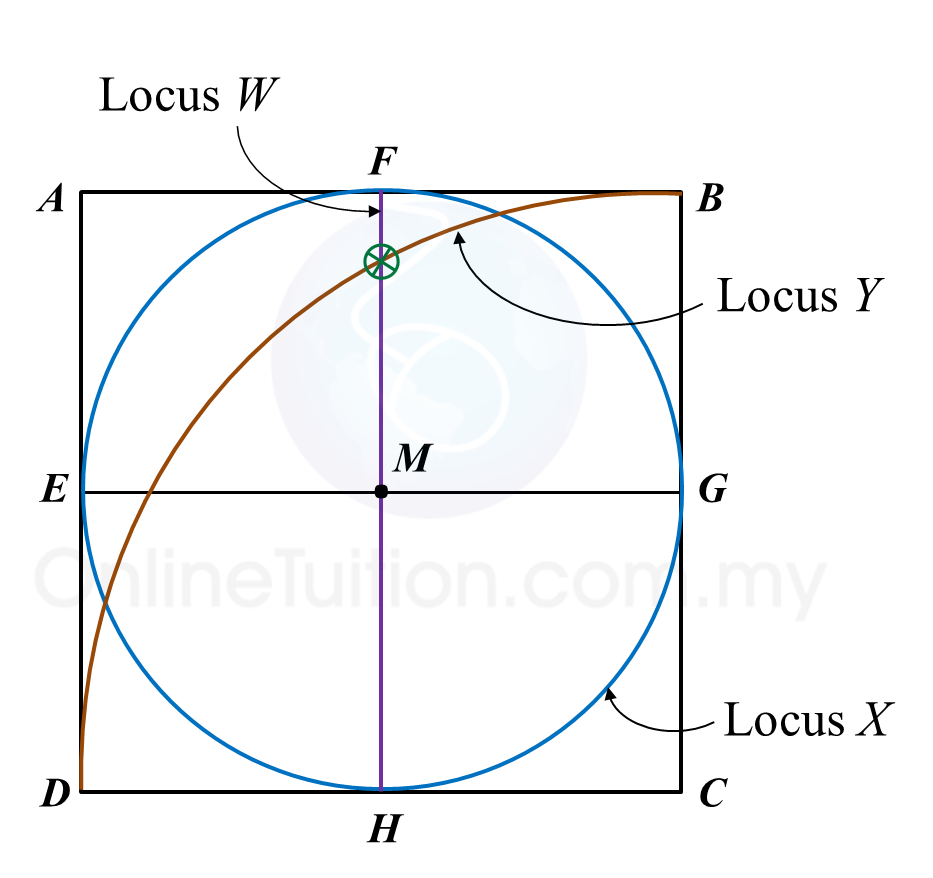
Diagram in the answer space below shows a square ABCD. E, F, G and H are the midpoints of straight lines AD, AB, BC and CD respectively. W, X and Y are moving points in the square.
On the diagram,
(a) draw the locus of the point W which moves such that it is always equidistant from point AD and BC.
(b) draw the locus of the point X which moves such that XM = MG.
(c) draw the locus of point Y which moves such that its distance is constantly 6 cm from point C.
(d) Hence, mark with the symbol ⊗ the intersection of the locus of W and the locus of Y.
Answer:
(a), (b), (c) and (d)
Solution: