Question 3 (a):
(i) Diagram 3.1 shows one of the methods of finding the highest common factor (HCF) and the lowest common multiples (LCM) for 12 and 32.
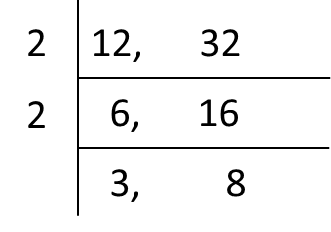Match the correct answer.
Answer:
(ii) The difference between two prime numbers is 9.
Write the two prime numbers in the answer space.
Answer:
( ) – ( ) = 9
Solution:
(i)
(ii)
( 11 ) – ( 2 ) = 9
(i) Diagram 3.1 shows one of the methods of finding the highest common factor (HCF) and the lowest common multiples (LCM) for 12 and 32.
Match the correct answer.Answer:
(ii) The difference between two prime numbers is 9.
Write the two prime numbers in the answer space.
Answer:
( ) – ( ) = 9
Solution:
(i)
(ii)
( 11 ) – ( 2 ) = 9
Question 3 (b):
Diagram 3.2 in the answer space shows a straight line JK.
(i) Using only a ruler and a pair of compasses, construct triangle JKL with KL = 8 cm and ∠JKL = 135o. You may begin from the straight line JK provided in the answer space.
Answer:
(ii) Measure KJL by using a protractor.
Solution:
(i)
(ii)
∠KJL = 26o
Diagram 3.2 in the answer space shows a straight line JK.
(i) Using only a ruler and a pair of compasses, construct triangle JKL with KL = 8 cm and ∠JKL = 135o. You may begin from the straight line JK provided in the answer space.
Answer:
(ii) Measure KJL by using a protractor.
Solution:
(i)
(ii)
∠KJL = 26o
Question 3 (c):
List all the integer values of x which satisfy the following linear inequalities:
–1 ≤ 1 + 2x < 5
Solution:
–1 ≤ 1 + 2x < 5
–1 ≤ 1 + 2x and 1 + 2x < 5
–2x ≤ 1 + 1 and 2x < 5 – 1
–2x ≤ 2 and 2x < 4
x ≥ –1 and x < 2
x = –1, 0, 1, 2, … and x = 1, 0, –1, –2 …
Thus x = –1, 0, 1.
List all the integer values of x which satisfy the following linear inequalities:
–1 ≤ 1 + 2x < 5
Solution:
–1 ≤ 1 + 2x < 5
–1 ≤ 1 + 2x and 1 + 2x < 5
–2x ≤ 1 + 1 and 2x < 5 – 1
–2x ≤ 2 and 2x < 4
x ≥ –1 and x < 2
x = –1, 0, 1, 2, … and x = 1, 0, –1, –2 …
Thus x = –1, 0, 1.