Question 7:
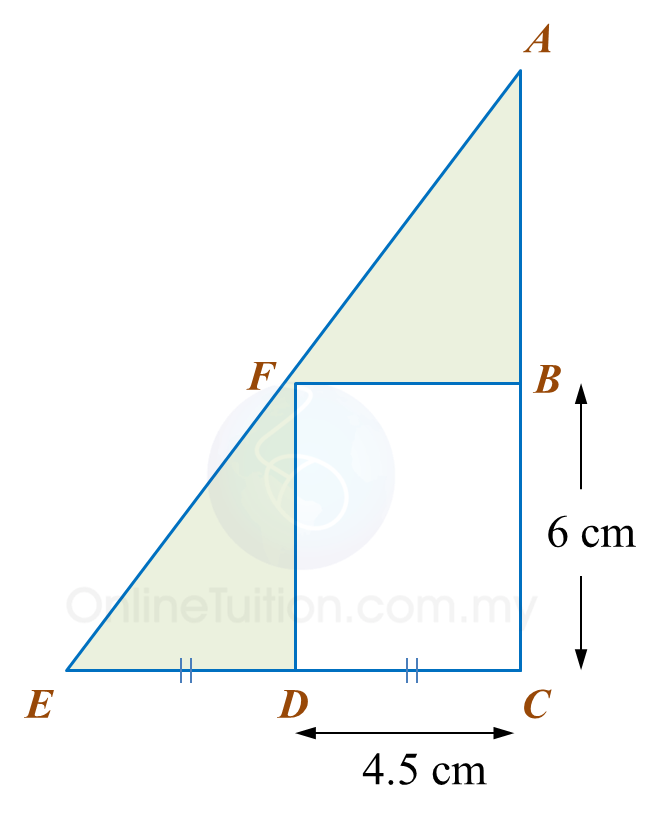
In diagram below, AEC is a right-angled triangle with an area of 54 cm2 and BCDF is a rectangle.
 Calculate
Calculate
(a) the perimeter, in cm, of the coloured region.
(b) the area, in cm2, of the coloured region.
Solution:
In diagram below, AEC is a right-angled triangle with an area of 54 cm2 and BCDF is a rectangle.
 Calculate
Calculate(a) the perimeter, in cm, of the coloured region.
(b) the area, in cm2, of the coloured region.
Solution:
Question 8:
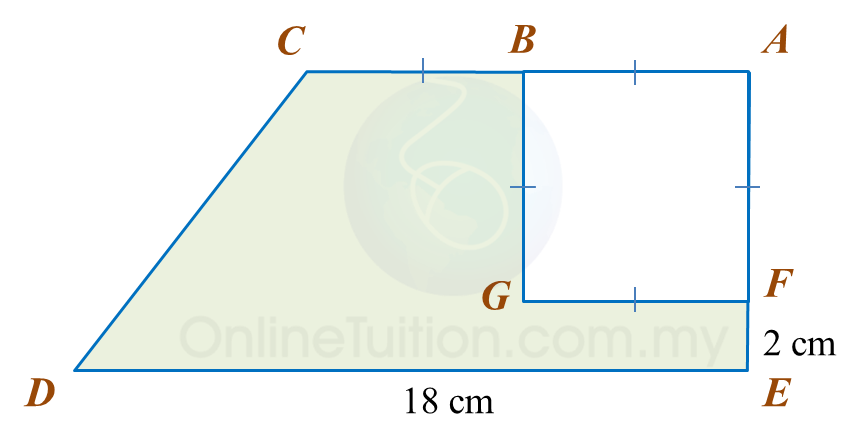
Diagram below shows a trapezium ABCDE. ABGF is a square with an area of 36 cm2.
Calculate
(a) the perimeter, in cm, of the coloured region.
(b) the area, in cm2, of the coloured region.
Solution:
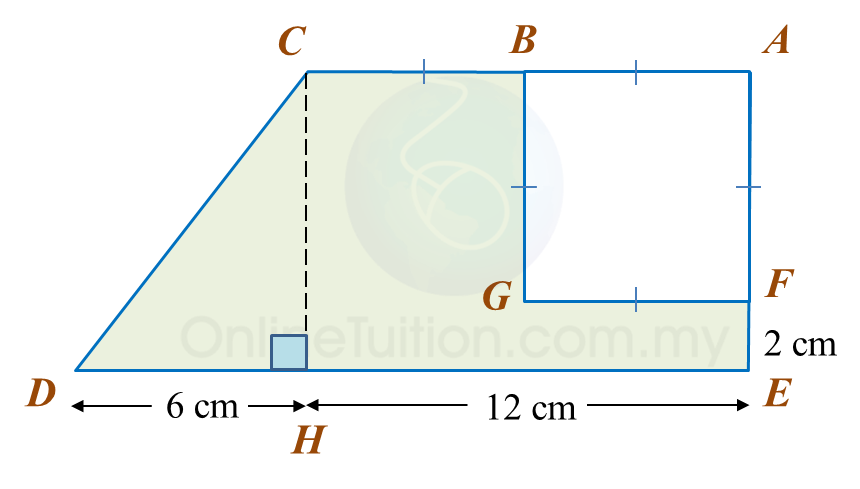
Diagram below shows a trapezium ABCDE. ABGF is a square with an area of 36 cm2.

Calculate
(a) the perimeter, in cm, of the coloured region.
(b) the area, in cm2, of the coloured region.
Solution:

Terima kasih banyak banyak