Question 1:
In the diagram, ABCD is a trapezium and ABEF is a parallelogram.
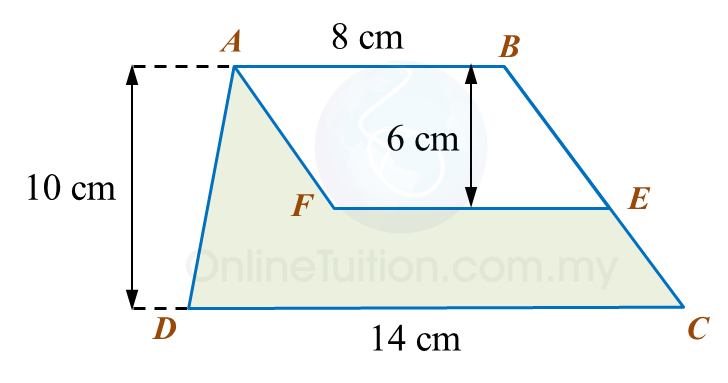 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.
Solution:
In the diagram, ABCD is a trapezium and ABEF is a parallelogram.
 Calculate the area, in cm2, of the coloured region.
Calculate the area, in cm2, of the coloured region.Solution:
Question 2:
Diagram below shows a rectangle ABCD.

Calculate the area, in cm2, of the coloured region.
Solution:
Diagram below shows a rectangle ABCD.

Calculate the area, in cm2, of the coloured region.
Solution:
Question 3:
In diagram below, ACEF is a trapezium and BCDG is a square.
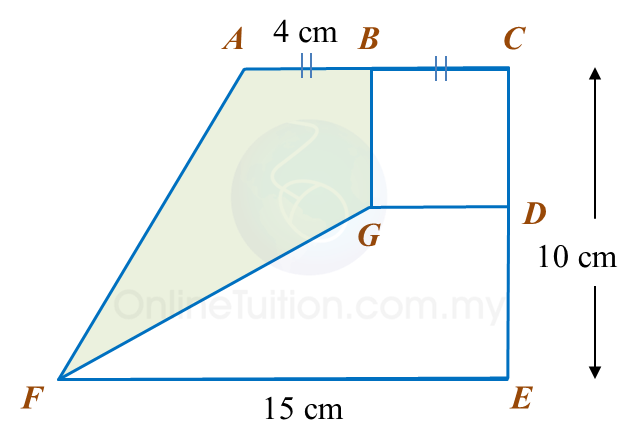
Calculate the area, in cm2, of the coloured region.
Solution:
In diagram below, ACEF is a trapezium and BCDG is a square.

Calculate the area, in cm2, of the coloured region.
Solution: