6.4.1 Surface Area of Three Dimensional Shapes, PT3 Focus Practice
Question 1:
Diagram below shows closed right cylinder.
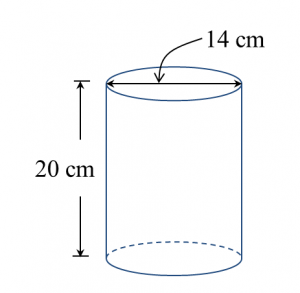

Calculate the total surface area, in cm2, of the cylinder.
Solution:
Total surface area
= 2(πr2) + 2πrh
Question 2:
Diagram below shows a right prism with right-angled triangle ABC as its uniform cross section.
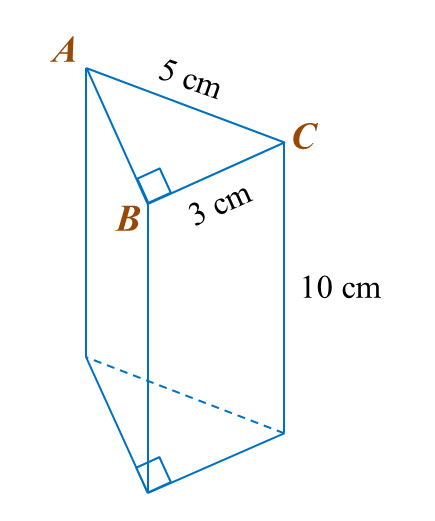

Calculate the total surface area, in cm2, of the prism.
Solution:
Total surface area
= 2 (½× 3 × 4) + (3 × 10) + (4 × 10) + (5 × 10)
= 12 + 30 + 40 + 50
= 132 cm2
Question 3:
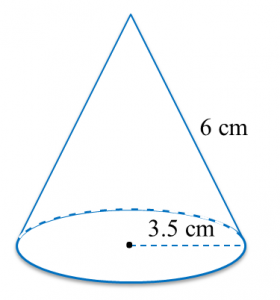
Solution:

The diagram shows a cone. The radius of its base is 3.5 cm and its slant height is 6 cm. Find the area of its curved surface.
( π= 22 7 )
( π= 22 7 )
Solution:
Area of curved surface
= π × radius of base × slant height
= πrs