6.2 Linear Equations
6.2.1 Linear Equations in Two Variables
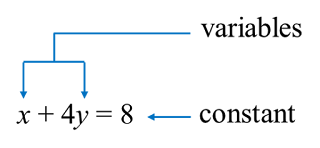
1. A linear equation in two variables is an equation which contains only linear terms and involves two variables.
2. If the value of one variable in an equation is known, then the value of the other variable can be determined and vice versa.
Example:
Given that 2x + 3y = 6, find the value of
(a) x when y = 4, (b) y when x = –3
Solution:
(a) Substitute y = 4 into the equation.
2x + 3y = 6
2x + 3 (4) = 6
2x + 12 = 6
2x = 6 – 12
2x = –6
x = –3
(b) Substitute x = –3 into the equation.
2x + 3y = 6
2 (–3) + 3y = 6
–6 + 3y = 6
3y = 6 + 6
3y = 12
y = 4
3. A linear equation in two variables has many possible solutions.