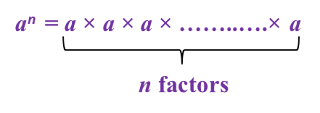4.1 Indices
1.1.1 Indices
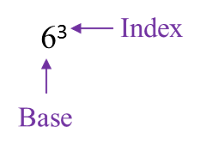
1. A number expressed in the form an is known as an index notation.
2. an is read as ‘a to the power of n’ where a is the base and n is the index.
Example:
3. If a is a real number and n is a positive integer, then
4. The value of a real number in index notation can be found by repeated multiplication.
Example:
64 = 6 × 6 × 6 × 6
= 1296
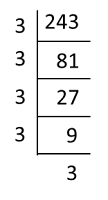
5. A number can be expressed in index notation by dividing the number repeatedly by the base.
Example:
243 = 3 × 3 × 3 × 3 × 3
1.1.2 Multiplication of Numbers in Index Notation
The multiplication of numbers or algebraic terms with the same base can be done by using the Law of Indices.
am × an = am + n
Example:
33 × 38 = 33+8
= 311
1.1.3 Division of Numbers in Index Notation
1. The Law of indices for division is:
am ÷ an = am - n
Example:
412 ÷ 412 = 412-12
= 40
= 1
2. a0 = 1
1.1.4 Raise Numbers and Algebraic Terms in Index Notation to a Power
To raise a number in index notation to a power, multiply the two indices while keeping the base unchanged.
(am ) n = (an ) m = amn
Example:
(43)7 = 43×7
= 4211.1.5 Negative Indices
Example:
1.1.6 Fractional Indices
Example: